Ralf Dragon
Dilemma First Search for Effortless Optimization of NP-Hard Problems
Sep 12, 2016
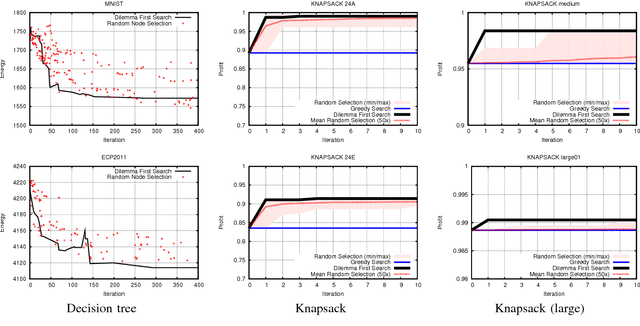

Abstract:To tackle the exponentiality associated with NP-hard problems, two paradigms have been proposed. First, Branch & Bound, like Dynamic Programming, achieve efficient exact inference but requires extensive information and analysis about the problem at hand. Second, meta-heuristics are easier to implement but comparatively inefficient. As a result, a number of problems have been left unoptimized and plain greedy solutions are used. We introduce a theoretical framework and propose a powerful yet simple search method called Dilemma First Search (DFS). DFS exploits the decision heuristic needed for the greedy solution for further optimization. DFS is useful when it is hard to design efficient exact inference. We evaluate DFS on two problems: First, the Knapsack problem, for which efficient algorithms exist, serves as a toy example. Second, Decision Tree inference, where state-of-the-art algorithms rely on the greedy or randomness-based solutions. We further show that decision trees benefit from optimizations that are performed in a fraction of the iterations required by a random-based search.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge