Raghav Kulkarni
Minwise-Independent Permutations with Insertion and Deletion of Features
Aug 22, 2023



Abstract:In their seminal work, Broder \textit{et. al.}~\citep{BroderCFM98} introduces the $\mathrm{minHash}$ algorithm that computes a low-dimensional sketch of high-dimensional binary data that closely approximates pairwise Jaccard similarity. Since its invention, $\mathrm{minHash}$ has been commonly used by practitioners in various big data applications. Further, the data is dynamic in many real-life scenarios, and their feature sets evolve over time. We consider the case when features are dynamically inserted and deleted in the dataset. We note that a naive solution to this problem is to repeatedly recompute $\mathrm{minHash}$ with respect to the updated dimension. However, this is an expensive task as it requires generating fresh random permutations. To the best of our knowledge, no systematic study of $\mathrm{minHash}$ is recorded in the context of dynamic insertion and deletion of features. In this work, we initiate this study and suggest algorithms that make the $\mathrm{minHash}$ sketches adaptable to the dynamic insertion and deletion of features. We show a rigorous theoretical analysis of our algorithms and complement it with extensive experiments on several real-world datasets. Empirically we observe a significant speed-up in the running time while simultaneously offering comparable performance with respect to running $\mathrm{minHash}$ from scratch. Our proposal is efficient, accurate, and easy to implement in practice.
Improving \textit{Tug-of-War} sketch using Control-Variates method
Mar 04, 2022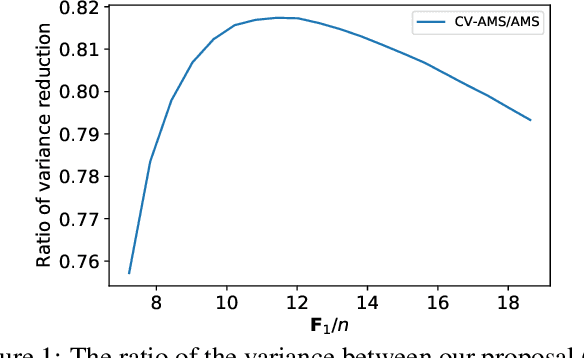



Abstract:Computing space-efficient summary, or \textit{a.k.a. sketches}, of large data, is a central problem in the streaming algorithm. Such sketches are used to answer \textit{post-hoc} queries in several data analytics tasks. The algorithm for computing sketches typically requires to be fast, accurate, and space-efficient. A fundamental problem in the streaming algorithm framework is that of computing the frequency moments of data streams. The frequency moments of a sequence containing $f_i$ elements of type $i$, are the numbers $\mathbf{F}_k=\sum_{i=1}^n {f_i}^k,$ where $i\in [n]$. This is also called as $\ell_k$ norm of the frequency vector $(f_1, f_2, \ldots f_n).$ Another important problem is to compute the similarity between two data streams by computing the inner product of the corresponding frequency vectors. The seminal work of Alon, Matias, and Szegedy~\cite{AMS}, \textit{a.k.a. Tug-of-war} (or AMS) sketch gives a randomized sublinear space (and linear time) algorithm for computing the frequency moments, and the inner product between two frequency vectors corresponding to the data streams. However, the variance of these estimates typically tends to be large. In this work, we focus on minimizing the variance of these estimates. We use the techniques from the classical Control-Variate method~\cite{Lavenberg} which is primarily known for variance reduction in Monte-Carlo simulations, and as a result, we are able to obtain significant variance reduction, at the cost of a little computational overhead. We present a theoretical analysis of our proposal and complement it with supporting experiments on synthetic as well as real-world datasets.
Efficient Compression Technique for Sparse Sets
Aug 16, 2017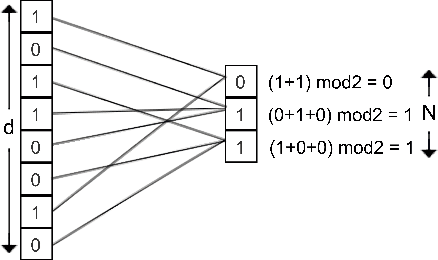
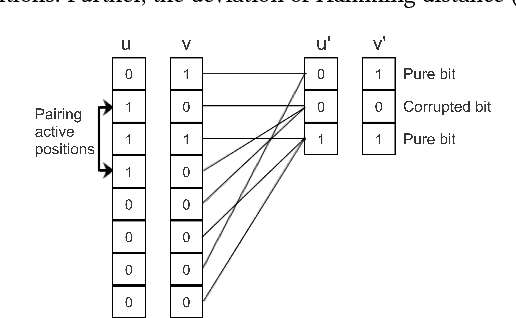
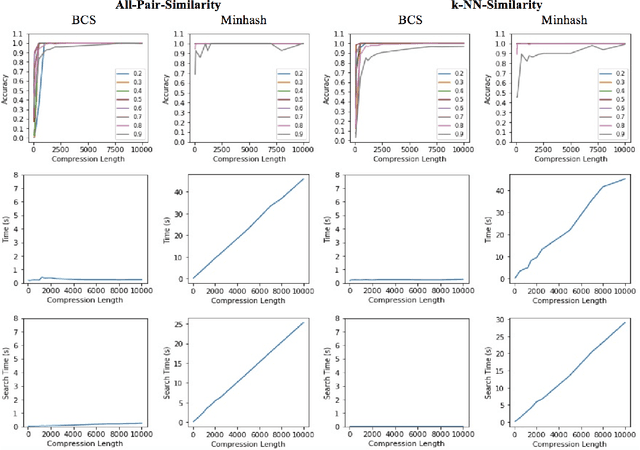
Abstract:Recent technological advancements have led to the generation of huge amounts of data over the web, such as text, image, audio and video. Most of this data is high dimensional and sparse, for e.g., the bag-of-words representation used for representing text. Often, an efficient search for similar data points needs to be performed in many applications like clustering, nearest neighbour search, ranking and indexing. Even though there have been significant increases in computational power, a simple brute-force similarity-search on such datasets is inefficient and at times impossible. Thus, it is desirable to get a compressed representation which preserves the similarity between data points. In this work, we consider the data points as sets and use Jaccard similarity as the similarity measure. Compression techniques are generally evaluated on the following parameters --1) Randomness required for compression, 2) Time required for compression, 3) Dimension of the data after compression, and 4) Space required to store the compressed data. Ideally, the compressed representation of the data should be such, that the similarity between each pair of data points is preserved, while keeping the time and the randomness required for compression as low as possible. We show that the compression technique suggested by Pratap and Kulkarni also works well for Jaccard similarity. We present a theoretical proof of the same and complement it with rigorous experimentations on synthetic as well as real-world datasets. We also compare our results with the state-of-the-art "min-wise independent permutation", and show that our compression algorithm achieves almost equal accuracy while significantly reducing the compression time and the randomness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge