Discovery of Dynamics Using Linear Multistep Methods

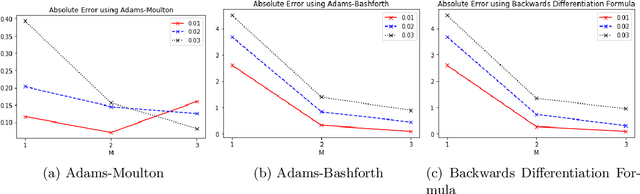
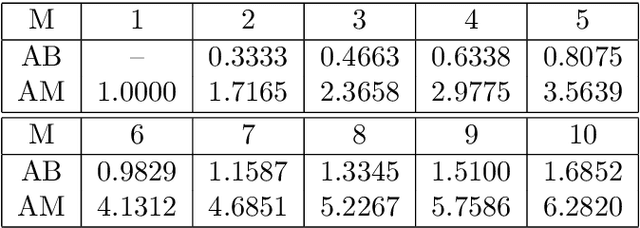
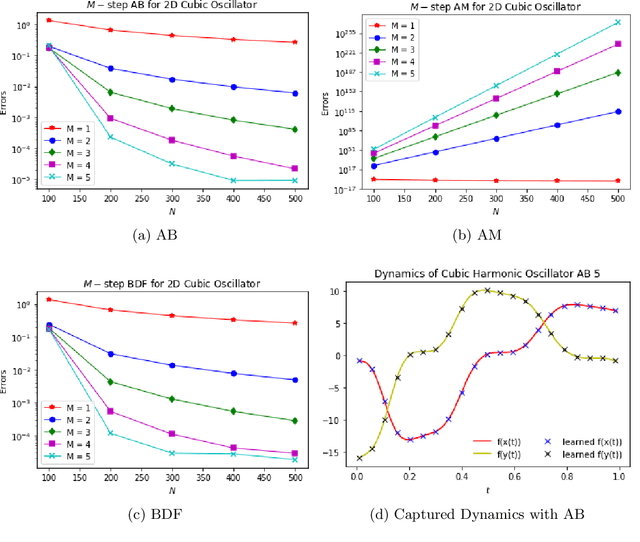
Linear multistep methods (LMMs) are popular time discretization techniques for the numerical solution of differential equations. Traditionally they are applied to solve for the state given the dynamics (the forward problem), but here we consider their application for learning the dynamics given the state (the inverse problem). This repurposing of LMMs is largely motivated by growing interest in data-driven modeling of dynamics, but the behavior and analysis of LMMs for discovery turn out to be significantly different from the well-known, existing theory for the forward problem. Assuming the highly idealized setting of being given the exact state, we establish for the first time a rigorous framework based on refined notions of consistency and stability to yield convergence using LMMs for discovery. When applying these concepts to three popular M-step LMMs, the Adams-Bashforth, Adams-Moulton, and Backwards Differentiation Formula schemes, the new theory suggests that Adams-Bashforth for $1 \leq M \leq 6$, Adams-Moulton for $M=0$ and $M=1$, and Backwards Differentiation Formula for $M \in \mathbb{N}$ are convergent, and, otherwise, the methods are not convergent in general. In addition, we provide numerical experiments to both motivate and substantiate our theoretical analysis.