Sampling Matters in Explanations: Towards Trustworthy Attribution Analysis Building Block in Visual Models through Maximizing Explanation Certainty

Image attribution analysis seeks to highlight the feature representations learned by visual models such that the highlighted feature maps can reflect the pixel-wise importance of inputs. Gradient integration is a building block in the attribution analysis by integrating the gradients from multiple derived samples to highlight the semantic features relevant to inferences. Such a building block often combines with other information from visual models such as activation or attention maps to form ultimate explanations. Yet, our theoretical analysis demonstrates that the extent to the alignment of the sample distribution in gradient integration with respect to natural image distribution gives a lower bound of explanation certainty. Prior works add noise into images as samples and the noise distributions can lead to low explanation certainty. Counter-intuitively, our experiment shows that extra information can saturate neural networks. To this end, building trustworthy attribution analysis needs to settle the sample distribution misalignment problem. Instead of adding extra information into input images, we present a semi-optimal sampling approach by suppressing features from inputs. The sample distribution by suppressing features is approximately identical to the distribution of natural images. Our extensive quantitative evaluation on large scale dataset ImageNet affirms that our approach is effective and able to yield more satisfactory explanations against state-of-the-art baselines throughout all experimental models.

Infinitesimal Higher-Order Spectral Variations in Rectangular Real Random Matrices

We present a theoretical framework for deriving the general $n$-th order Fr\'echet derivatives of singular values in real rectangular matrices, by leveraging reduced resolvent operators from Kato's analytic perturbation theory for self-adjoint operators. Deriving closed-form expressions for higher-order derivatives of singular values is notoriously challenging through standard matrix-analysis techniques. To overcome this, we treat a real rectangular matrix as a compact operator on a finite-dimensional Hilbert space, and embed the rectangular matrix into a block self-adjoint operator so that non-symmetric perturbations are captured. Applying Kato's asymptotic eigenvalue expansion to this construction, we obtain a general, closed-form expression for the infinitesimal $n$-th order spectral variations. Specializing to $n=2$ and deploying on a Kronecker-product representation with matrix convention yield the Hessian of a singular value, not found in literature. By bridging abstract operator-theoretic perturbation theory with matrices, our framework equips researchers with a practical toolkit for higher-order spectral sensitivity studies in random matrix applications (e.g., adversarial perturbation in deep learning).

Interpreting Global Perturbation Robustness of Image Models using Axiomatic Spectral Importance Decomposition

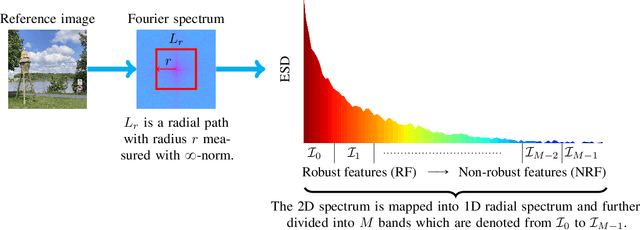
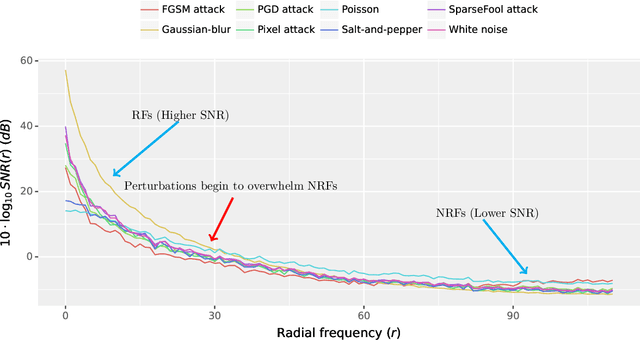
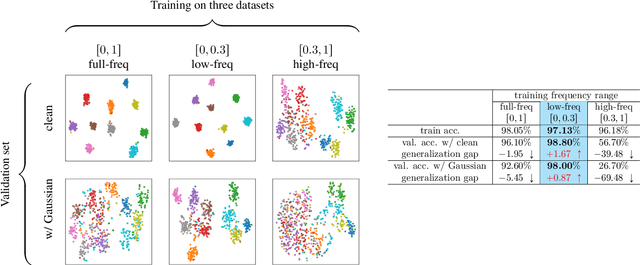
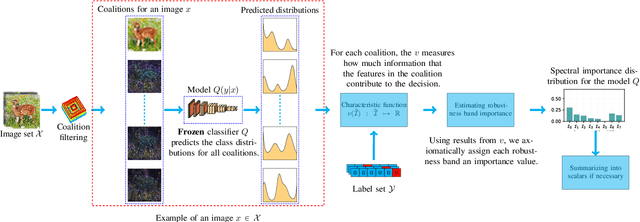
Perturbation robustness evaluates the vulnerabilities of models, arising from a variety of perturbations, such as data corruptions and adversarial attacks. Understanding the mechanisms of perturbation robustness is critical for global interpretability. We present a model-agnostic, global mechanistic interpretability method to interpret the perturbation robustness of image models. This research is motivated by two key aspects. First, previous global interpretability works, in tandem with robustness benchmarks, e.g. mean corruption error (mCE), are not designed to directly interpret the mechanisms of perturbation robustness within image models. Second, we notice that the spectral signal-to-noise ratios (SNR) of perturbed natural images exponentially decay over the frequency. This power-law-like decay implies that: Low-frequency signals are generally more robust than high-frequency signals -- yet high classification accuracy can not be achieved by low-frequency signals alone. By applying Shapley value theory, our method axiomatically quantifies the predictive powers of robust features and non-robust features within an information theory framework. Our method, dubbed as \textbf{I-ASIDE} (\textbf{I}mage \textbf{A}xiomatic \textbf{S}pectral \textbf{I}mportance \textbf{D}ecomposition \textbf{E}xplanation), provides a unique insight into model robustness mechanisms. We conduct extensive experiments over a variety of vision models pre-trained on ImageNet to show that \textbf{I-ASIDE} can not only \textbf{measure} the perturbation robustness but also \textbf{provide interpretations} of its mechanisms.

Reclaiming Residual Knowledge: A Novel Paradigm to Low-Bit Quantization

This paper explores a novel paradigm in low-bit (i.e. 4-bits or lower) quantization, differing from existing state-of-the-art methods, by framing optimal quantization as an architecture search problem within convolutional neural networks (ConvNets). Our framework, dubbed \textbf{CoRa} (Optimal Quantization Residual \textbf{Co}nvolutional Operator Low-\textbf{Ra}nk Adaptation), is motivated by two key aspects. Firstly, quantization residual knowledge, i.e. the lost information between floating-point weights and quantized weights, has long been neglected by the research community. Reclaiming the critical residual knowledge, with an infinitesimal extra parameter cost, can reverse performance degradation without training. Secondly, state-of-the-art quantization frameworks search for optimal quantized weights to address the performance degradation. Yet, the vast search spaces in weight optimization pose a challenge for the efficient optimization in large models. For example, state-of-the-art BRECQ necessitates $2 \times 10^4$ iterations to quantize models. Fundamentally differing from existing methods, \textbf{CoRa} searches for the optimal architectures of low-rank adapters, reclaiming critical quantization residual knowledge, within the search spaces smaller compared to the weight spaces, by many orders of magnitude. The low-rank adapters approximate the quantization residual weights, discarded in previous methods. We evaluate our approach over multiple pre-trained ConvNets on ImageNet. \textbf{CoRa} achieves comparable performance against both state-of-the-art quantization-aware training and post-training quantization baselines, in $4$-bit and $3$-bit quantization, by using less than $250$ iterations on a small calibration set with $1600$ images. Thus, \textbf{CoRa} establishes a new state-of-the-art in terms of the optimization efficiency in low-bit quantization.