Qing Chuan Ye
Fair task allocation in transportation
Dec 07, 2016
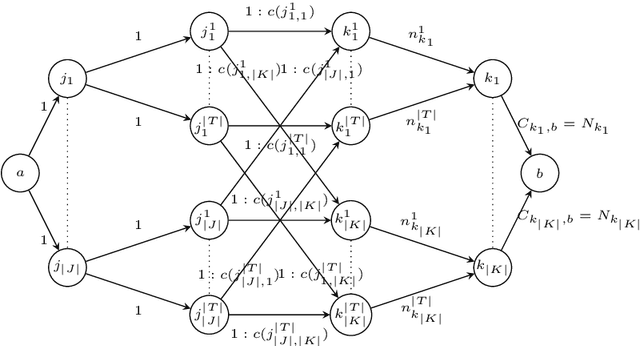


Abstract:Task allocation problems have traditionally focused on cost optimization. However, more and more attention is being given to cases in which cost should not always be the sole or major consideration. In this paper we study a fair task allocation problem in transportation where an optimal allocation not only has low cost but more importantly, it distributes tasks as even as possible among heterogeneous participants who have different capacities and costs to execute tasks. To tackle this fair minimum cost allocation problem we analyze and solve it in two parts using two novel polynomial-time algorithms. We show that despite the new fairness criterion, the proposed algorithms can solve the fair minimum cost allocation problem optimally in polynomial time. In addition, we conduct an extensive set of experiments to investigate the trade-off between cost minimization and fairness. Our experimental results demonstrate the benefit of factoring fairness into task allocation. Among the majority of test instances, fairness comes with a very small price in terms of cost.
Learning optimization models in the presence of unknown relations
Apr 15, 2014



Abstract:In a sequential auction with multiple bidding agents, it is highly challenging to determine the ordering of the items to sell in order to maximize the revenue due to the fact that the autonomy and private information of the agents heavily influence the outcome of the auction. The main contribution of this paper is two-fold. First, we demonstrate how to apply machine learning techniques to solve the optimal ordering problem in sequential auctions. We learn regression models from historical auctions, which are subsequently used to predict the expected value of orderings for new auctions. Given the learned models, we propose two types of optimization methods: a black-box best-first search approach, and a novel white-box approach that maps learned models to integer linear programs (ILP) which can then be solved by any ILP-solver. Although the studied auction design problem is hard, our proposed optimization methods obtain good orderings with high revenues. Our second main contribution is the insight that the internal structure of regression models can be efficiently evaluated inside an ILP solver for optimization purposes. To this end, we provide efficient encodings of regression trees and linear regression models as ILP constraints. This new way of using learned models for optimization is promising. As the experimental results show, it significantly outperforms the black-box best-first search in nearly all settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge