Distributed Learning of Generalized Linear Causal Networks

We consider the task of learning causal structures from data stored on multiple machines, and propose a novel structure learning method called distributed annealing on regularized likelihood score (DARLS) to solve this problem. We model causal structures by a directed acyclic graph that is parameterized with generalized linear models, so that our method is applicable to various types of data. To obtain a high-scoring causal graph, DARLS simulates an annealing process to search over the space of topological sorts, where the optimal graphical structure compatible with a sort is found by a distributed optimization method. This distributed optimization relies on multiple rounds of communication between local and central machines to estimate the optimal structure. We establish its convergence to a global optimizer of the overall score that is computed on all data across local machines. To the best of our knowledge, DARLS is the first distributed method for learning causal graphs with such theoretical guarantees. Through extensive simulation studies, DARLS has shown competing performance against existing methods on distributed data, and achieved comparable structure learning accuracy and test-data likelihood with competing methods applied to pooled data across all local machines. In a real-world application for modeling protein-DNA binding networks with distributed ChIP-Sequencing data, DARLS also exhibits higher predictive power than other methods, demonstrating a great advantage in estimating causal networks from distributed data.

Optimizing regularized Cholesky score for order-based learning of Bayesian networks

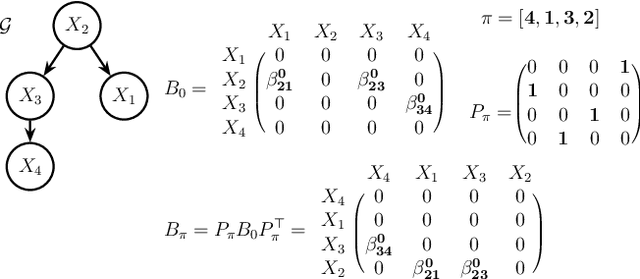
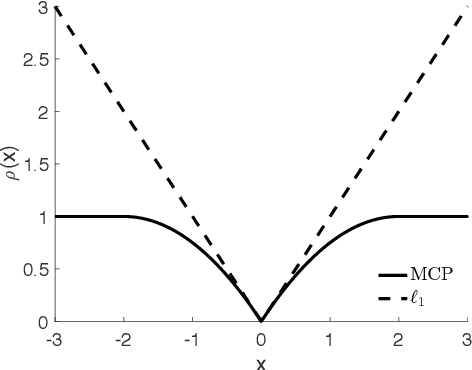
Bayesian networks are a class of popular graphical models that encode causal and conditional independence relations among variables by directed acyclic graphs (DAGs). We propose a novel structure learning method, annealing on regularized Cholesky score (ARCS), to search over topological sorts, or permutations of nodes, for a high-scoring Bayesian network. Our scoring function is derived from regularizing Gaussian DAG likelihood, and its optimization gives an alternative formulation of the sparse Cholesky factorization problem from a statistical viewpoint, which is of independent interest. We combine global simulated annealing over permutations with a fast proximal gradient algorithm, operating on triangular matrices of edge coefficients, to compute the score of any permutation. Combined, the two approaches allow us to quickly and effectively search over the space of DAGs without the need to verify the acyclicity constraint or to enumerate possible parent sets given a candidate topological sort. The annealing aspect of the optimization is able to consistently improve the accuracy of DAGs learned by local search algorithms. In addition, we develop several techniques to facilitate the structure learning, including pre-annealing data-driven tuning parameter selection and post-annealing constraint-based structure refinement. Through extensive numerical comparisons, we show that ARCS achieves substantial improvements over existing methods, demonstrating its great potential to learn Bayesian networks from both observational and experimental data.