Parallel Simulation of Contact and Actuation for Soft Growing Robots

Soft growing robots, commonly referred to as vine robots, have demonstrated remarkable ability to interact safely and robustly with unstructured and dynamic environments. It is therefore natural to exploit contact with the environment for planning and design optimization tasks. Previous research has focused on planning under contact for passively deforming robots with pre-formed bends. However, adding active steering to these soft growing robots is necessary for successful navigation in more complex environments. To this end, we develop a unified modeling framework that integrates vine robot growth, bending, actuation, and obstacle contact. We extend the beam moment model to include the effects of actuation on kinematics under growth and then use these models to develop a fast parallel simulation framework. We validate our model and simulator with real robot experiments. To showcase the capabilities of our framework, we apply our model in a design optimization task to find designs for vine robots navigating through cluttered environments, identifying designs that minimize the number of required actuators by exploiting environmental contacts. We show the robustness of the designs to environmental and manufacturing uncertainties. Finally, we fabricate an optimized design and successfully deploy it in an obstacle-rich environment.

Physical Reservoir Computing with Origami and its Application to Robotic Crawling

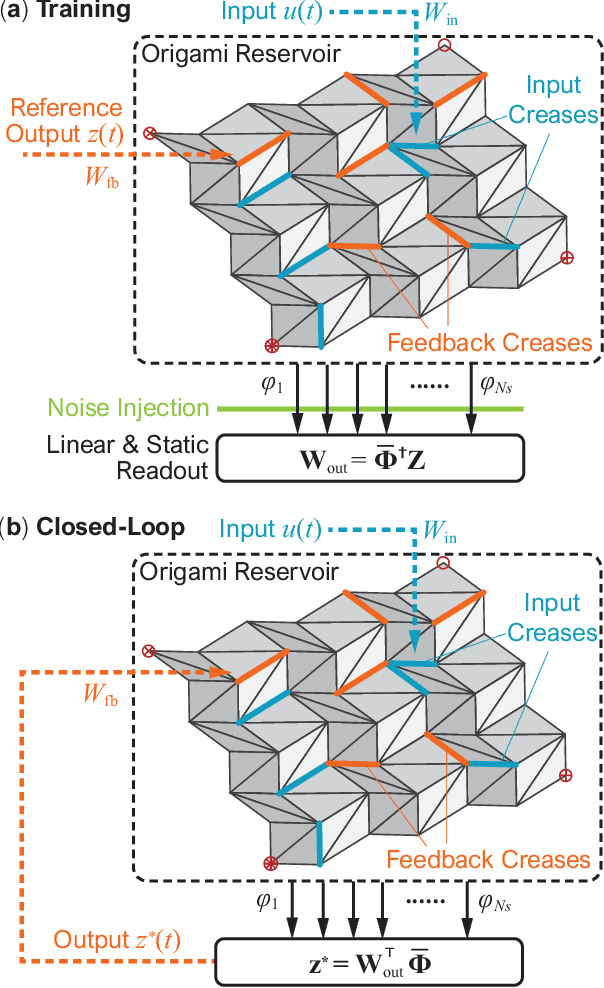
A new paradigm called physical reservoir computing has recently emerged, where the nonlinear dynamics of high-dimensional and fixed physical systems are harnessed as a computational resource to achieve complex tasks. Via extensive simulations based on a dynamic truss-frame model, this study shows that an origami structure can perform as a dynamic reservoir with sufficient computing power to emulate high-order nonlinear systems, generate stable limit cycles, and modulate outputs according to dynamic inputs. This study also uncovers the linkages between the origami reservoir's physical designs and its computing power, offering a guideline to optimize the computing performance. Comprehensive parametric studies show that selecting optimal feedback crease distribution and fine-tuning the underlying origami folding designs are the most effective approach to improve computing performance. Furthermore, this study shows how origami's physical reservoir computing power can apply to soft robotic control problems by a case study of earthworm-like peristaltic crawling without traditional controllers. These results can pave the way for origami-based robots with embodied mechanical intelligence.

Peristaltic locomotion without digital controllers: Exploiting the origami multi-stability to coordinate robotic motions

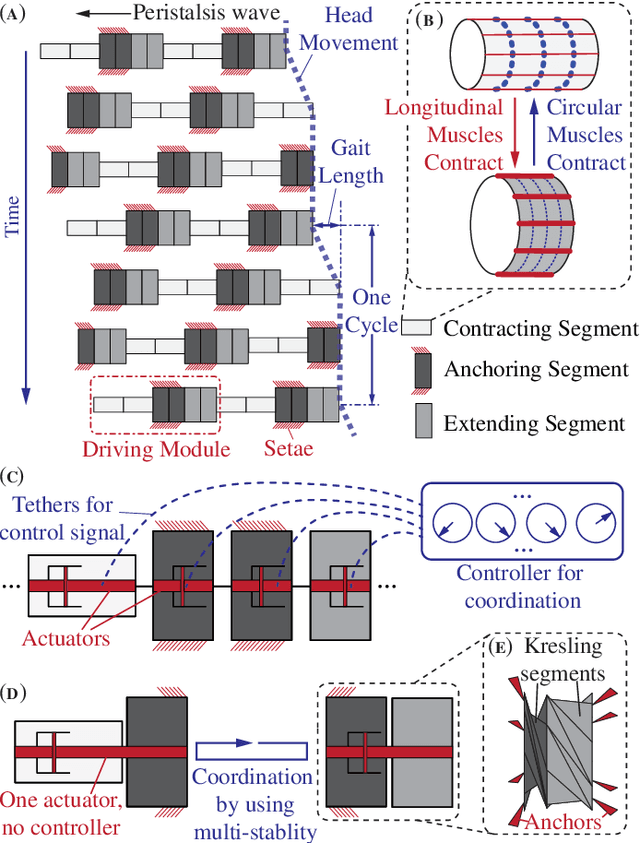
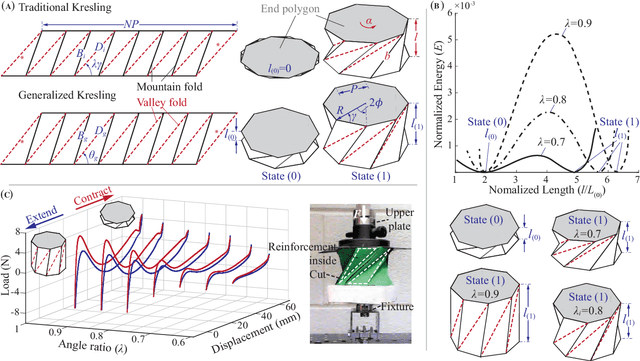
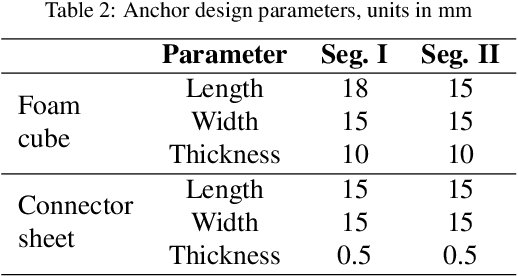
This study proposes and examines a novel approach to generate peristaltic-like locomotion in a segmented origami robot. Specifically, we demonstrate the use of multi-stability embedded in origami skeleton to eliminate the need for multiple actuators or digital controllers to coordinate the complex robotic movements in peristaltic crawling. The crawling robot in this study consists of two serially connected bistable origami segments, each featuring a generalized Kresling design and a foldable anchoring mechanism. Mechanics analysis and experimental testing of this dual-segment module reveal a deterministic deformation sequence or actuation cycle, which is then used to generate the different phases in a peristaltic-like locomotion gait. Instead of individually controlling the segment deformation like in earthworm and other crawling robots, we only control the total length of this robot. Therefore, this approach can significantly reduce the total number of actuators needed for locomotion and simplify the control requirements. Moreover, the richness in Kresling origami design offers us substantial freedom to tailor the locomotion performance. Results of this study will contribute to a paradigm shift in how we can use the mechanics of multi-stability for robotic actuation and control.