Praveen Chandrasekhar
Iterative Surrogate Model Optimization (ISMO): An active learning algorithm for PDE constrained optimization with deep neural networks
Aug 13, 2020


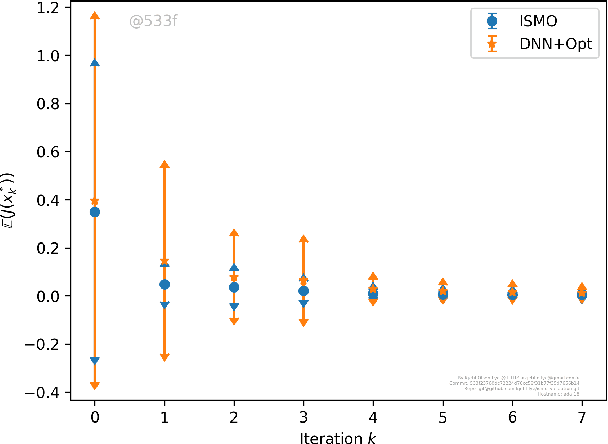
Abstract:We present a novel active learning algorithm, termed as iterative surrogate model optimization (ISMO), for robust and efficient numerical approximation of PDE constrained optimization problems. This algorithm is based on deep neural networks and its key feature is the iterative selection of training data through a feedback loop between deep neural networks and any underlying standard optimization algorithm. Under suitable hypotheses, we show that the resulting optimizers converge exponentially fast (and with exponentially decaying variance), with respect to increasing number of training samples. Numerical examples for optimal control, parameter identification and shape optimization problems for PDEs are provided to validate the proposed theory and to illustrate that ISMO significantly outperforms a standard deep neural network based surrogate optimization algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge