Density Estimation from Schlieren Images through Machine Learning

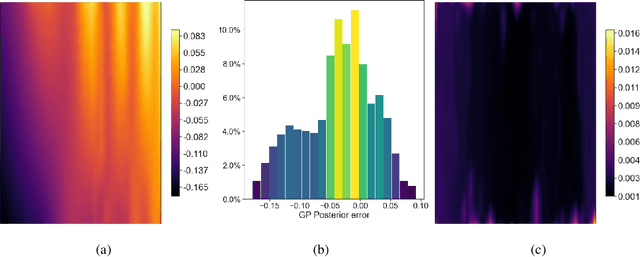
This study proposes a radically alternate approach for extracting quantitative information from schlieren images. The method uses a scaled, derivative enhanced Gaussian process model to obtain true density estimates from two corresponding schlieren images with the knife-edge at horizontal and vertical orientations. We illustrate our approach on schlieren images taken from a wind tunnel sting model, and a supersonic aircraft in flight.

Automatic Borescope Damage Assessments for Gas Turbine Blades via Deep Learning

To maximise fuel economy, bladed components in aero-engines operate close to material limits. The severe operating environment leads to in-service damage on compressor and turbine blades, having a profound and immediate impact on the performance of the engine. Current methods of blade visual inspection are mainly based on borescope imaging. During these inspections, the sentencing of components under inspection requires significant manual effort, with a lack of systematic approaches to avoid human biases. To perform fast and accurate sentencing, we propose an automatic workflow based on deep learning for detecting damage present on rotor blades using borescope videos. Building upon state-of-the-art methods from computer vision, we show that damage statistics can be presented for each blade in a blade row separately, and demonstrate the workflow on two borescope videos.

Supporting Multi-point Fan Design with Dimension Reduction

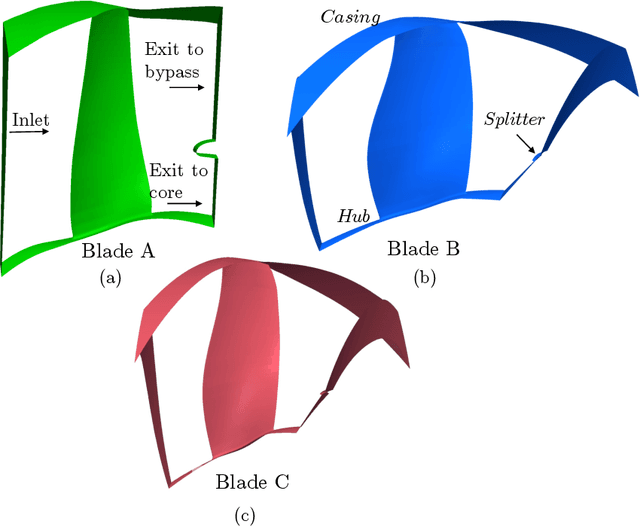
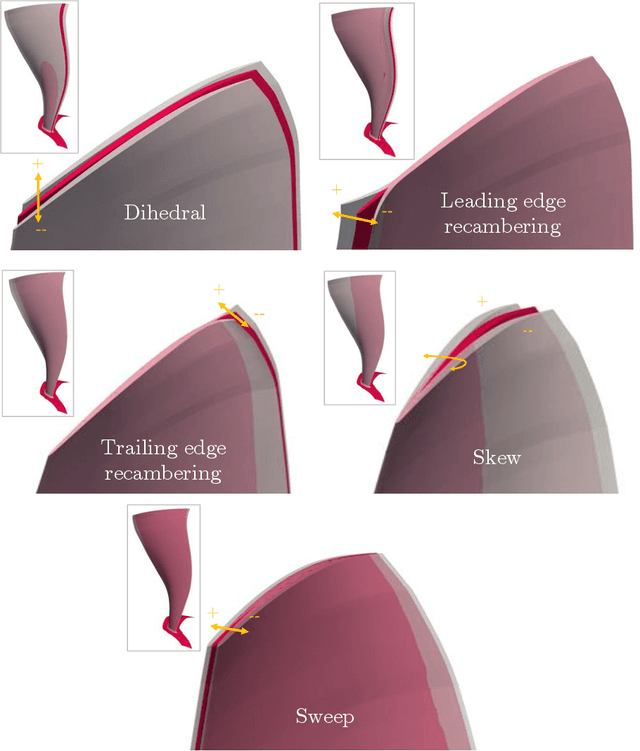
Motivated by the idea of turbomachinery active subspace performance maps, this paper studies dimension reduction in turbomachinery 3D CFD simulations. First, we show that these subspaces exist across different blades---under the same parametrization---largely independent of their Mach number or Reynolds number. This is demonstrated via a numerical study on three different blades. Then, in an attempt to reduce the computational cost of identifying a suitable dimension reducing subspace, we examine statistical sufficient dimension reduction methods, including sliced inverse regression, sliced average variance estimation, principal Hessian directions and contour regression. Unsatisfied by these results, we evaluate a new idea based on polynomial variable projection---a non-linear least squares problem. Our results using polynomial variable projection clearly demonstrate that one can accurately identify dimension reducing subspaces for turbomachinery functionals at a fraction of the cost associated with prior methods. We apply these subspaces to the problem of comparing design configurations across different flight points on a working line of a fan blade. We demonstrate how designs that offer a healthy compromise between performance at cruise and sea-level conditions can be easily found by visually inspecting their subspaces.