Physics-Aware Tensor Reconstruction for Radio Maps in Pixel-Based Fluid Antenna Systems

The deployment of pixel-based antennas and fluid antenna systems (FAS) is hindered by prohibitive channel state information (CSI) acquisition overhead. While radio maps enable proactive mode selection, reconstructing high-fidelity maps from sparse measurements is challenging. Existing physics-agnostic or data-driven methods often fail to recover fine-grained shadowing details under extreme sparsity. We propose a Physics-Regularized Low-Rank Tensor Completion (PR-LRTC) framework for radio map reconstruction. By modeling the signal field as a three-way tensor, we integrate environmental low-rankness with deterministic antenna physics. Specifically, we leverage Effective Aerial Degrees-of-Freedom (EADoF) theory to derive a differential gain topology map as a physical prior for regularization. The resulting optimization problem is solved via an efficient Alternating Direction Method of Multipliers (ADMM)-based algorithm. Simulations show that PR-LRTC achieves a 4 dB gain over baselines at a 10% sampling ratio. It effectively preserves sharp shadowing edges, providing a robust, physics-compliant solution for low-overhead beam management.

Geometry-Aligned Differential Privacy for Location-Safe Federated Radio Map Construction

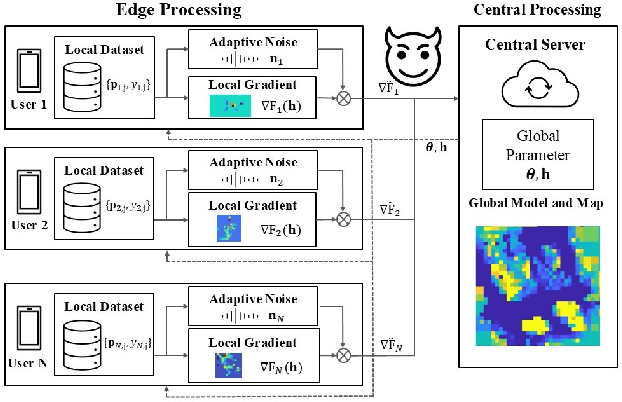
Radio maps that describe spatial variations in wireless signal strength are widely used to optimize networks and support aerial platforms. Their construction requires location-labeled signal measurements from distributed users, raising fundamental concerns about location privacy. Even when raw data are kept local, the shared model updates can reveal user locations through their spatial structure, while naive noise injection either fails to hide this leakage or degrades model accuracy. This work analyzes how location leakage arises from gradients in a virtual-environment radio map model and proposes a geometry-aligned differential privacy mechanism with heterogeneous noise tailored to both confuse localization and cover gradient spatial patterns. The approach is theoretically supported with a convergence guarantee linking privacy strength to learning accuracy. Numerical experiments show the approach increases attacker localization error from 30 m to over 180 m, with only 0.2 dB increase in radio map construction error compared to a uniform-noise baseline.

Optimum Noncoherent Detection of Constant-Envelope Signals using Received Signal Magnitudes -- Energy Detection and Amplitude Detection

Constant-envelope signals are widely employed in wireless communication systems due to their hardware-friendly design, energy efficiency, and enhanced reliability. However, detecting these signals reliably using simple, power-efficient receivers remains a critical challenge. While coherent detection methods generally offer superior performance, they require complex frequency synchronization, which increases receiver complexity and power consumption. In contrast, noncoherent detection is inherently simpler since it avoids frequency synchronization. However, traditional noncoherent detection approaches still rely on In-phase and Quadrature-phase (IQ) demodulators to extract the noisy received signal magnitudes, and assume the energy detector as the test statistic according to the IQ structure, without rigorous theoretical justification. Motivated by the practical need for robust and low-complexity detection, this paper proposes a comprehensive framework for optimal signal detection using a simple bandpass-filter envelope-detector (BFED) in conjunction with a Bayesian approach and the generalized likelihood ratio test (GLRT) under unknown amplitude conditions. By leveraging approximations of the modified Bessel functions, we derive two distinct regimes of the optimal detector. In the low SNR regime, we rigorously prove that the energy detector emerges as the Bayesian-optimal solution, thereby establishing its theoretical validity for the first time. In the high SNR regime, we derive a novel amplitude-based detector that directly compares the estimated amplitude against the noise standard deviation, leading to a simple yet optimal detection strategy. Numerical simulations validate the theoretical findings, confirming that both the energy and amplitude detectors achieve the minimum error probability in their respective SNR domains.