Optimal Full Ranking from Pairwise Comparisons

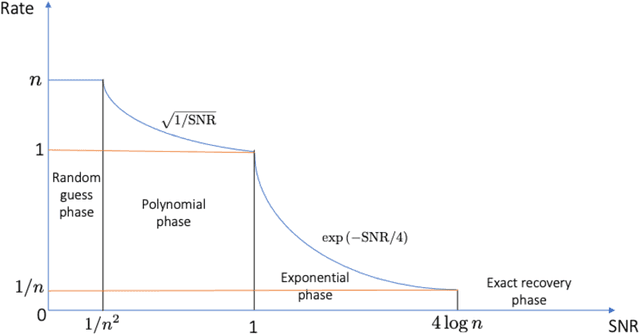
We consider the problem of ranking $n$ players from partial pairwise comparison data under the Bradley-Terry-Luce model. For the first time in the literature, the minimax rate of this ranking problem is derived with respect to the Kendall's tau distance that measures the difference between two rank vectors by counting the number of inversions. The minimax rate of ranking exhibits a transition between an exponential rate and a polynomial rate depending on the magnitude of the signal-to-noise ratio of the problem. To the best of our knowledge, this phenomenon is unique to full ranking and has not been seen in any other statistical estimation problem. To achieve the minimax rate, we propose a divide-and-conquer ranking algorithm that first divides the $n$ players into groups of similar skills and then computes local MLE within each group. The optimality of the proposed algorithm is established by a careful approximate independence argument between the two steps.

Partial Recovery for Top-$k$ Ranking: Optimality of MLE and Sub-Optimality of Spectral Method

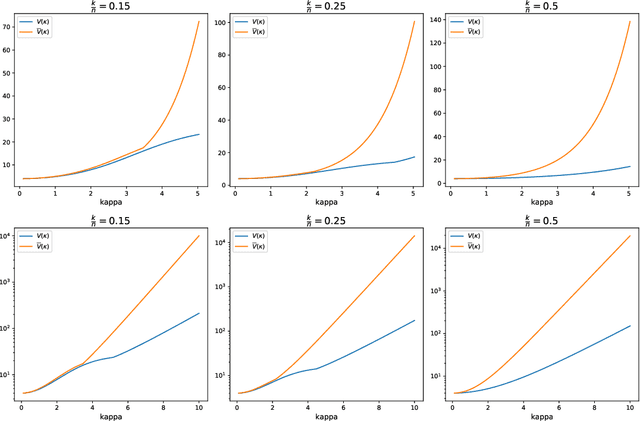
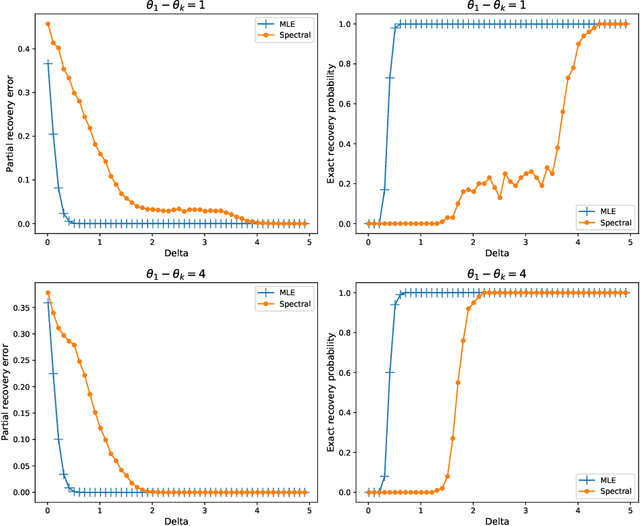
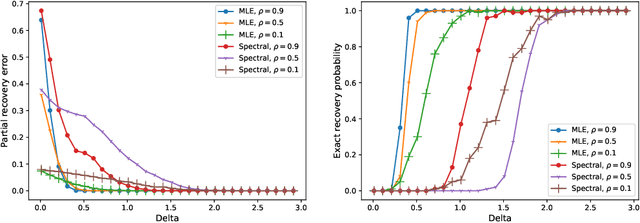
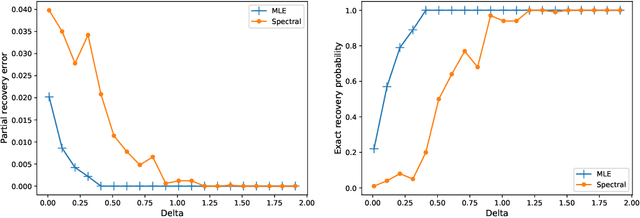
Given partially observed pairwise comparison data generated by the Bradley-Terry-Luce (BTL) model, we study the problem of top-$k$ ranking. That is, to optimally identify the set of top-$k$ players. We derive the minimax rate with respect to a normalized Hamming loss. This provides the first result in the literature that characterizes the partial recovery error in terms of the proportion of mistakes for top-$k$ ranking. We also derive the optimal signal to noise ratio condition for the exact recovery of the top-$k$ set. The maximum likelihood estimator (MLE) is shown to achieve both optimal partial recovery and optimal exact recovery. On the other hand, we show another popular algorithm, the spectral method, is in general sub-optimal. Our results complement the recent work by Chen et al. (2019) that shows both the MLE and the spectral method achieve the optimal sample complexity for exact recovery. It turns out the leading constants of the sample complexity are different for the two algorithms. Another contribution that may be of independent interest is the analysis of the MLE without any penalty or regularization for the BTL model. This closes an important gap between theory and practice in the literature of ranking.