Optimal Full Ranking from Pairwise Comparisons
Paper and Code
Jan 21, 2021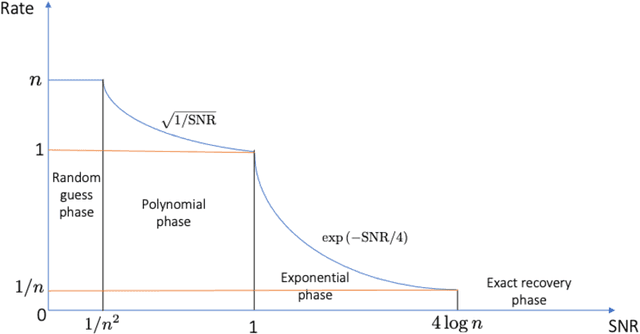
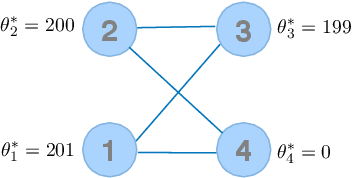
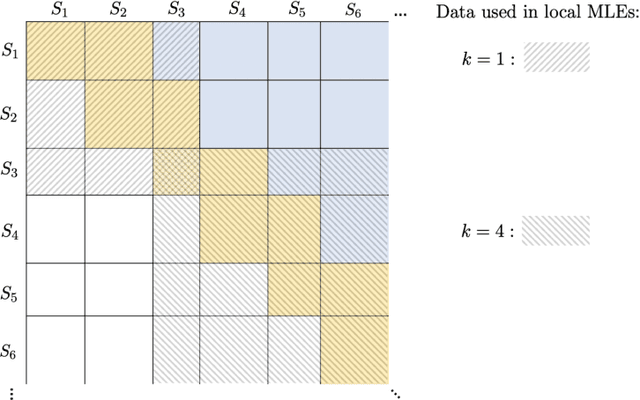
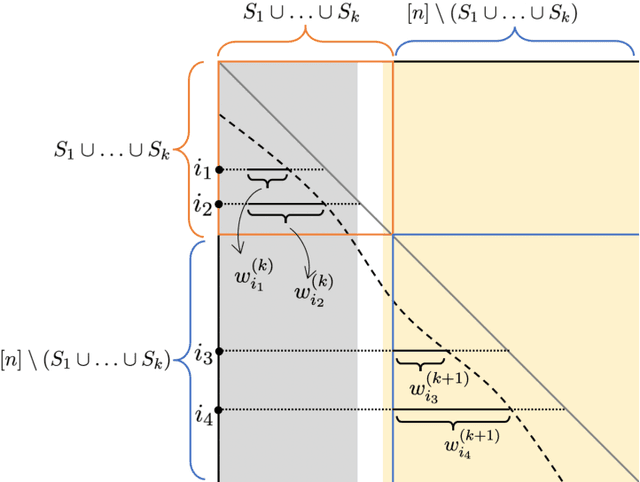
We consider the problem of ranking $n$ players from partial pairwise comparison data under the Bradley-Terry-Luce model. For the first time in the literature, the minimax rate of this ranking problem is derived with respect to the Kendall's tau distance that measures the difference between two rank vectors by counting the number of inversions. The minimax rate of ranking exhibits a transition between an exponential rate and a polynomial rate depending on the magnitude of the signal-to-noise ratio of the problem. To the best of our knowledge, this phenomenon is unique to full ranking and has not been seen in any other statistical estimation problem. To achieve the minimax rate, we propose a divide-and-conquer ranking algorithm that first divides the $n$ players into groups of similar skills and then computes local MLE within each group. The optimality of the proposed algorithm is established by a careful approximate independence argument between the two steps.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge