Philippe R. Richard
Université de Montréal
Automating the Generation of High School Geometry Proofs using Prolog in an Educational Context
Feb 28, 2020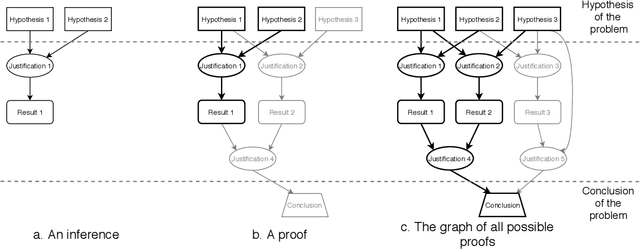

Abstract:When working on intelligent tutor systems designed for mathematics education and its specificities, an interesting objective is to provide relevant help to the students by anticipating their next steps. This can only be done by knowing, beforehand, the possible ways to solve a problem. Hence the need for an automated theorem prover that provide proofs as they would be written by a student. To achieve this objective, logic programming is a natural tool due to the similarity of its reasoning with a mathematical proof by inference. In this paper, we present the core ideas we used to implement such a prover, from its encoding in Prolog to the generation of the complete set of proofs. However, when dealing with educational aspects, there are many challenges to overcome. We also present the main issues we encountered, as well as the chosen solutions.
* In Proceedings ThEdu'19, arXiv:2002.11895
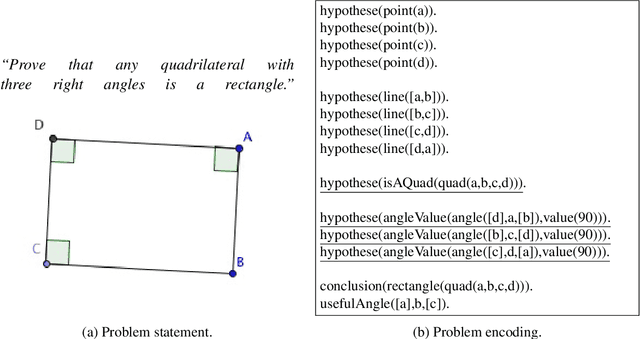
Improving QED-Tutrix by Automating the Generation of Proofs
Mar 05, 2018
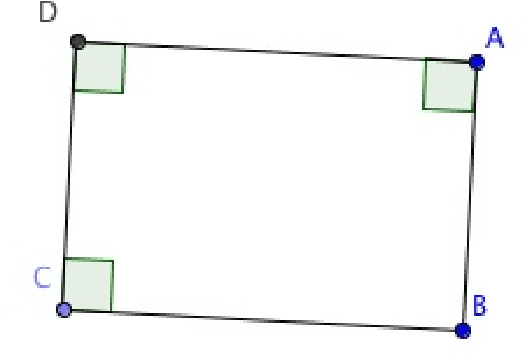
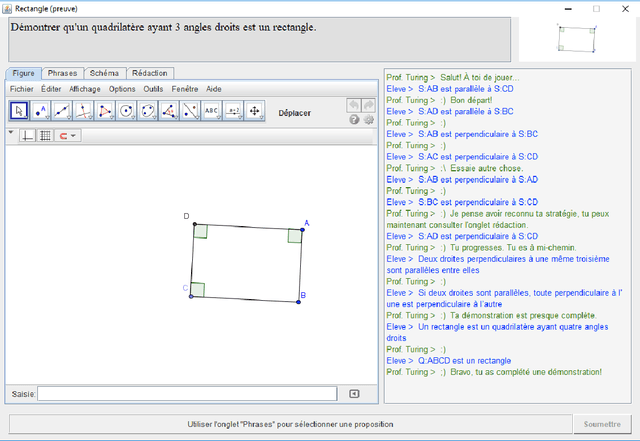
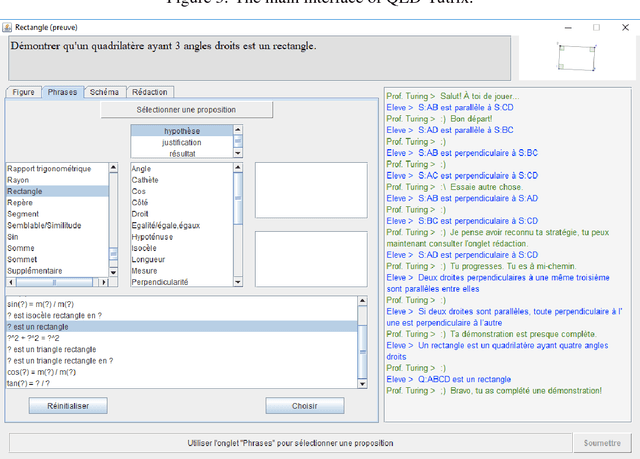
Abstract:The idea of assisting teachers with technological tools is not new. Mathematics in general, and geometry in particular, provide interesting challenges when developing educative softwares, both in the education and computer science aspects. QED-Tutrix is an intelligent tutor for geometry offering an interface to help high school students in the resolution of demonstration problems. It focuses on specific goals: 1) to allow the student to freely explore the problem and its figure, 2) to accept proofs elements in any order, 3) to handle a variety of proofs, which can be customized by the teacher, and 4) to be able to help the student at any step of the resolution of the problem, if the need arises. The software is also independent from the intervention of the teacher. QED-Tutrix offers an interesting approach to geometry education, but is currently crippled by the lengthiness of the process of implementing new problems, a task that must still be done manually. Therefore, one of the main focuses of the QED-Tutrix' research team is to ease the implementation of new problems, by automating the tedious step of finding all possible proofs for a given problem. This automation must follow fundamental constraints in order to create problems compatible with QED-Tutrix: 1) readability of the proofs, 2) accessibility at a high school level, and 3) possibility for the teacher to modify the parameters defining the "acceptability" of a proof. We present in this paper the result of our preliminary exploration of possible avenues for this task. Automated theorem proving in geometry is a widely studied subject, and various provers exist. However, our constraints are quite specific and some adaptation would be required to use an existing prover. We have therefore implemented a prototype of automated prover to suit our needs. The future goal is to compare performances and usability in our specific use-case between the existing provers and our implementation.
* In Proceedings ThEdu'17, arXiv:1803.00722
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge