Statistical monitoring of models based on artificial intelligence

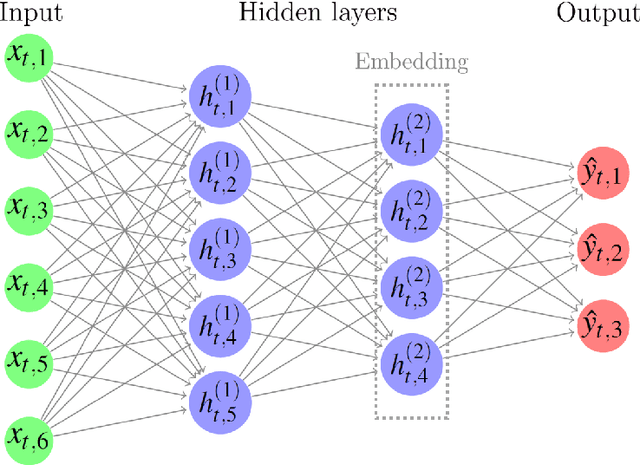
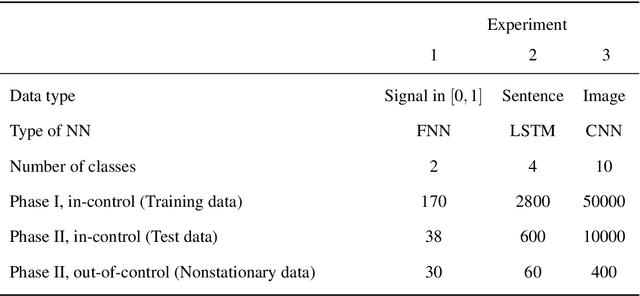
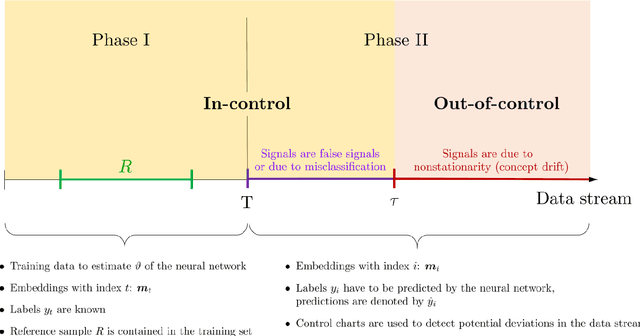
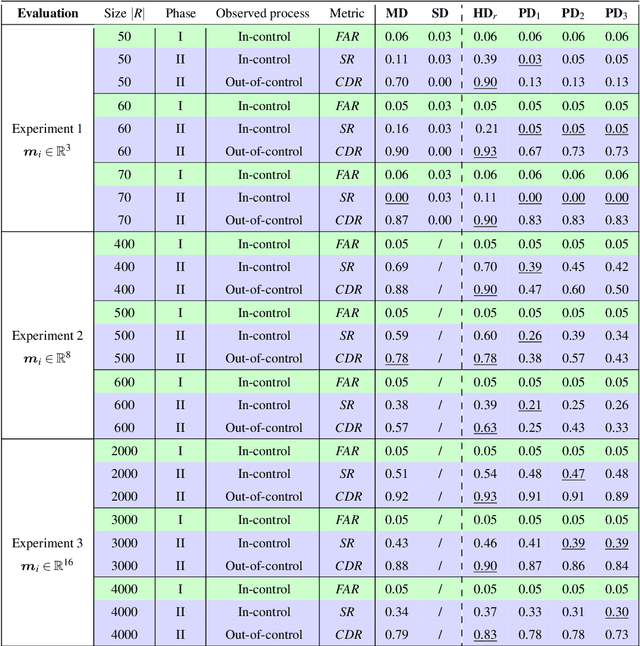
The rapid advancement of models based on artificial intelligence demands innovative monitoring techniques which can operate in real time with low computational costs. In machine learning, especially if we consider neural network (NN) learning algorithms, and in particular deep-learning architectures, the models are often trained in a supervised manner. Consequently, the learned relationship between the input and the output must remain valid during the model's deployment. If this stationarity assumption holds, we can conclude that the NN generates accurate predictions. Otherwise, the retraining or rebuilding of the model is required. We propose to consider the latent feature representation of the data (called "embedding") generated by the NN for determining the time point when the data stream starts being nonstationary. To be precise, we monitor embeddings by applying multivariate control charts based on the calculation of the data depth and normalized ranks. The performance of the introduced method is evaluated using various NNs with different underlying data formats.

Adaptive LASSO estimation for functional hidden dynamic geostatistical model

We propose a novel model selection algorithm based on a penalized maximum likelihood estimator (PMLE) for functional hidden dynamic geostatistical models (f-HDGM). These models employ a classic mixed-effect regression structure with embedded spatiotemporal dynamics to model georeferenced data observed in a functional domain. Thus, the parameters of interest are functions across this domain. The algorithm simultaneously selects the relevant spline basis functions and regressors that are used to model the fixed-effects relationship between the response variable and the covariates. In this way, it automatically shrinks to zero irrelevant parts of the functional coefficients or the entire effect of irrelevant regressors. The algorithm is based on iterative optimisation and uses an adaptive least absolute shrinkage and selector operator (LASSO) penalty function, wherein the weights are obtained by the unpenalised f-HDGM maximum-likelihood estimators. The computational burden of maximisation is drastically reduced by a local quadratic approximation of the likelihood. Through a Monte Carlo simulation study, we analysed the performance of the algorithm under different scenarios, including strong correlations among the regressors. We showed that the penalised estimator outperformed the unpenalised estimator in all the cases we considered. We applied the algorithm to a real case study in which the recording of the hourly nitrogen dioxide concentrations in the Lombardy region in Italy was modelled as a functional process with several weather and land cover covariates.

Statistical learning for change point and anomaly detection in graphs

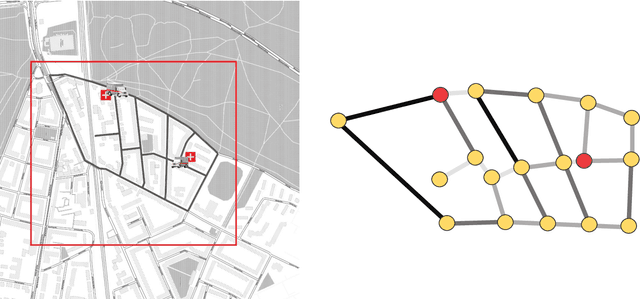
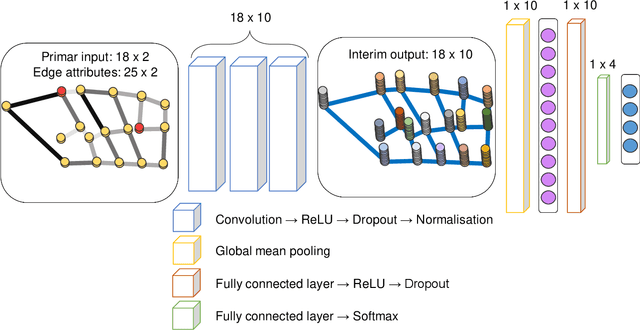
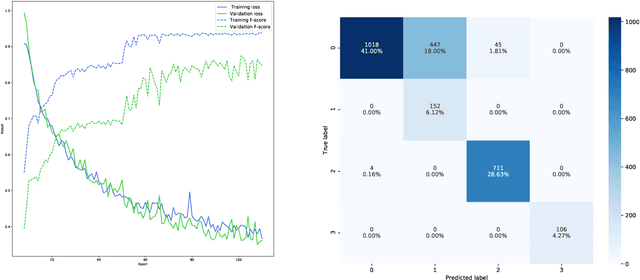
Complex systems which can be represented in the form of static and dynamic graphs arise in different fields, e.g. communication, engineering and industry. One of the interesting problems in analysing dynamic network structures is to monitor changes in their development. Statistical learning, which encompasses both methods based on artificial intelligence and traditional statistics, can be used to progress in this research area. However, the majority of approaches apply only one or the other framework. In this paper, we discuss the possibility of bringing together both disciplines in order to create enhanced network monitoring procedures focussing on the example of combining statistical process control and deep learning algorithms. Together with the presentation of change point and anomaly detection in network data, we propose to monitor the response times of ambulance services, applying jointly the control chart for quantile function values and a graph convolutional network.

Estimation of the spatial weighting matrix for regular lattice data -- An adaptive lasso approach with cross-sectional resampling

Spatial econometric research typically relies on the assumption that the spatial dependence structure is known in advance and is represented by a deterministic spatial weights matrix. Contrary to classical approaches, we investigate the estimation of sparse spatial dependence structures for regular lattice data. In particular, an adaptive least absolute shrinkage and selection operator (lasso) is used to select and estimate the individual connections of the spatial weights matrix. To recover the spatial dependence structure, we propose cross-sectional resampling, assuming that the random process is exchangeable. The estimation procedure is based on a two-step approach to circumvent simultaneity issues that typically arise from endogenous spatial autoregressive dependencies. The two-step adaptive lasso approach with cross-sectional resampling is verified using Monte Carlo simulations. Eventually, we apply the procedure to model nitrogen dioxide ($\mathrm{NO_2}$) concentrations and show that estimating the spatial dependence structure contrary to using prespecified weights matrices improves the prediction accuracy considerably.