Energy-Aware Bayesian Control Barrier Functions for Physics-Informed Gaussian Process Dynamics

We study safe control for dynamical systems whose continuous-time dynamics are learned with Gaussian processes (GPs), focusing on mechanical and port-Hamiltonian systems where safety is naturally expressed via energy constraints. The availability of a GP Hamiltonian posterior naturally raises the question of how to systematically exploit this structure to design an energy-aware control barrier function with high-probability safety guarantees. We address this problem by developing a Bayesian-CBF framework and instantiating it with energy-aware Bayesian-CBFs (EB-CBFs) that construct conservative energy-based barriers directly from the Hamiltonian and vector-field posteriors, yielding safety filters that minimally modify a nominal controller while providing probabilistic energy safety guarantees. Numerical simulations on a mass-spring system demonstrate that the proposed EB-CBFs achieve high-probability safety under noisy sampled GP-learned dynamics.

Safe Reference Tracking and Collision Avoidance for Taxiing Aircraft Using an MPC-CBF Framework

In this paper, we develop a framework for the automatic taxiing of aircraft between hangar and take-off given a graph-based model of an airport. We implement a high-level path-planning algorithm that models taxiway intersections as nodes in an undirected graph, algorithmically constructs a directed graph according to the physical limitations of the aircraft, and finds the shortest valid taxi path through the directed graph using Dijkstra's algorithm. We then use this shortest path to construct a reference trajectory for the aircraft to follow that considers the turning capabilities of a given aircraft. Using high-order control barrier functions (HOCBFs), we construct safety conditions for multi-obstacle avoidance and safe reference tracking for simple 2D unicycle dynamics with acceleration control inputs. We then use these safety conditions to design an MPC-CBF framework that tracks the reference trajectory while adhering to the safety constraints. We compare the performance of our MPC-CBF controller with a PID-CBF control method via simulations.

Collaborative Safety-Critical Formation Control with Obstacle Avoidance

This work explores a collaborative method for ensuring safety in multi-agent formation control problems. We formulate a control barrier function (CBF) based safety filter control law for a generic distributed formation controller and extend our previously developed collaborative safety framework to an obstacle avoidance problem for agents with acceleration control inputs. We then incorporate multi-obstacle collision avoidance into the collaborative safety framework. This framework includes a method for computing the maximum capability of agents to satisfy their individual safety requirements. We analyze the convergence rate of our collaborative safety algorithm, and prove the linear-time convergence of cooperating agents to a jointly feasible safe action for all agents under the special case of a tree-structured communication network with a single obstacle for each agent. We illustrate the analytical results via simulation on a mass-spring kinematics-based formation controller and demonstrate the finite-time convergence of the collaborative safety algorithm in the simple proven case, the more general case of a fully-connected system with multiple static obstacles, and with dynamic obstacles.

Modeling and Predicting Epidemic Spread: A Gaussian Process Regression Approach

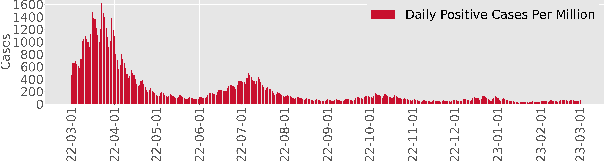
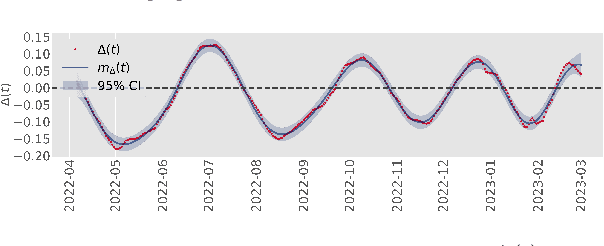
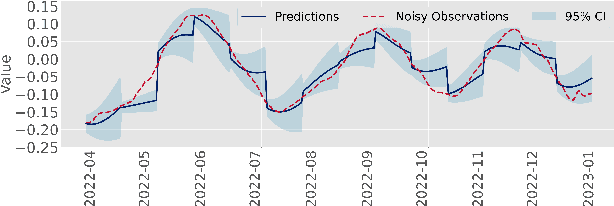
Modeling and prediction of epidemic spread are critical to assist in policy-making for mitigation. Therefore, we present a new method based on Gaussian Process Regression to model and predict epidemics, and it quantifies prediction confidence through variance and high probability error bounds. Gaussian Process Regression excels in using small datasets and providing uncertainty bounds, and both of these properties are critical in modeling and predicting epidemic spreading processes with limited data. However, the derivation of formal uncertainty bounds remains lacking when using Gaussian Process Regression in the setting of epidemics, which limits its usefulness in guiding mitigation efforts. Therefore, in this work, we develop a novel bound on the variance of the prediction that quantifies the impact of the epidemic data on the predictions we make. Further, we develop a high probability error bound on the prediction, and we quantify how the epidemic spread, the infection data, and the length of the prediction horizon all affect this error bound. We also show that the error stays below a certain threshold based on the length of the prediction horizon. To illustrate this framework, we leverage Gaussian Process Regression to model and predict COVID-19 using real-world infection data from the United Kingdom.

Collaborative Safe Formation Control for Coupled Multi-Agent Systems

The safe control of multi-robot swarms is a challenging and active field of research, where common goals include maintaining group cohesion while simultaneously avoiding obstacles and inter-agent collision. Building off our previously developed theory for distributed collaborative safety-critical control for networked dynamic systems, we propose a distributed algorithm for the formation control of robot swarms given individual agent dynamics, induced formation dynamics, and local neighborhood position and velocity information within a defined sensing radius for each agent. Individual safety guarantees for each agent are obtained using rounds of communication between neighbors to restrict unsafe control actions among cooperating agents through safety conditions derived from high-order control barrier functions (CBFs). We provide conditions under which a swarm is guaranteed to achieve collective safety with respect to multiple obstacles using a modified collaborative safety algorithm. We demonstrate the performance of our distributed algorithm via simulation in a simplified physics-based environment.