Deep Learning Classification of 3.5 GHz Band Spectrograms with Applications to Spectrum Sensing

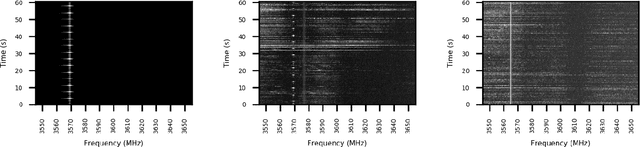
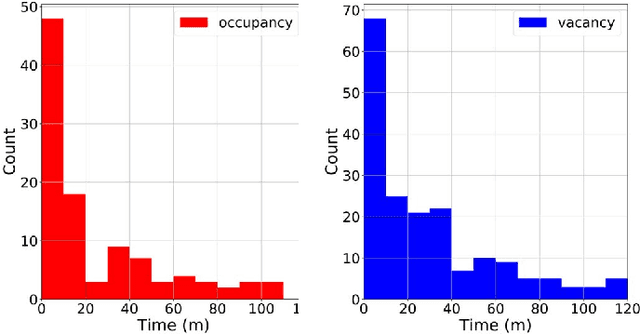
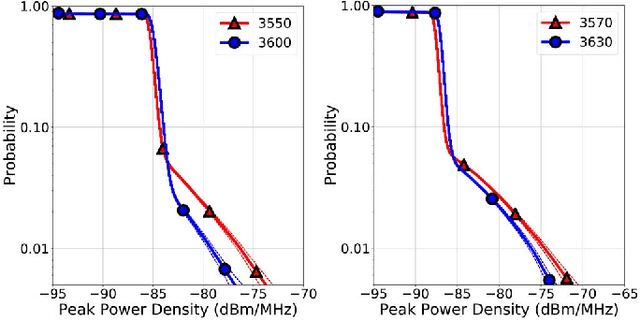
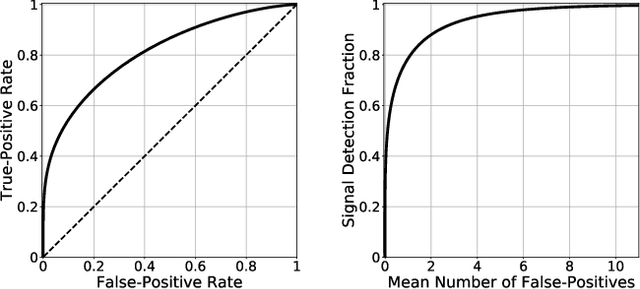
In the United States, the Federal Communications Commission has adopted rules permitting commercial wireless networks to share spectrum with federal incumbents in the 3.5 GHz Citizens Broadband Radio Service band (3550-3700 MHz). These rules require commercial wireless systems to vacate the band when coastal sensor networks detect radars operated by the U.S. military; a key example being the SPN-43 air traffic control radar. For such coastal sensor networks to meet their operating requirements, they require highly-accurate detection algorithms. In addition to their use in sensor networks, detection algorithms can assist in the generation of descriptive statistics for libraries of spectrum recordings. In this paper, using a library of over 14,000 3.5 GHz band spectrograms collected by a recent measurement campaign, we investigate the performance of three different methods for SPN-43 radar detection. Namely, we compare classical energy detection to two deep learning algorithms: a convolutional neural network and a long short-term memory recurrent neural network. Performing a thorough evaluation, we demonstrate that deep learning algorithms appreciably outperform energy detection. Finally, we apply the best-performing classifier to generate descriptive statistics for the 3.5 GHz spectrogram library. Overall, our findings highlight potential weaknesses of energy detection as well as the strengths of modern deep learning algorithms for radar detection in the 3.5 GHz band.

Local Consistency and SAT-Solvers

Local consistency techniques such as k-consistency are a key component of specialised solvers for constraint satisfaction problems. In this paper we show that the power of using k-consistency techniques on a constraint satisfaction problem is precisely captured by using a particular inference rule, which we call negative-hyper-resolution, on the standard direct encoding of the problem into Boolean clauses. We also show that current clause-learning SAT-solvers will discover in expected polynomial time any inconsistency that can be deduced from a given set of clauses using negative-hyper-resolvents of a fixed size. We combine these two results to show that, without being explicitly designed to do so, current clause-learning SAT-solvers efficiently simulate k-consistency techniques, for all fixed values of k. We then give some experimental results to show that this feature allows clause-learning SAT-solvers to efficiently solve certain families of constraint problems which are challenging for conventional constraint-programming solvers.