Explicitly Solvable Continuous-time Inference for Partially Observed Markov Processes

Many natural and engineered systems can be modeled as discrete state Markov processes. Often, only a subset of states are directly observable. Inferring the conditional probability that a system occupies a particular hidden state, given the partial observation, is a problem with broad application. In this paper, we introduce a continuous-time formulation of the sum-product algorithm, which is a well-known discrete-time method for finding the hidden states' conditional probabilities, given a set of finite, discrete-time observations. From our new formulation, we can explicitly solve for the conditional probability of occupying any state, given the transition rates and observations within a finite time window. We apply our algorithm to a realistic model of the cystic fibrosis transmembrane conductance regulator (CFTR) protein for exact inference of the conditional occupancy probability, given a finite time series of partial observations.

A factor graph EM algorithm for inference of kinetic microstates from patch clamp measurements

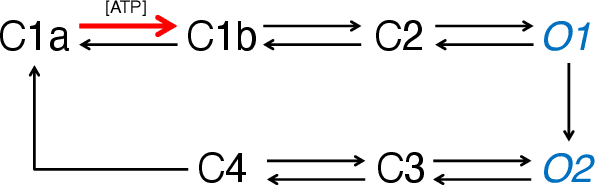
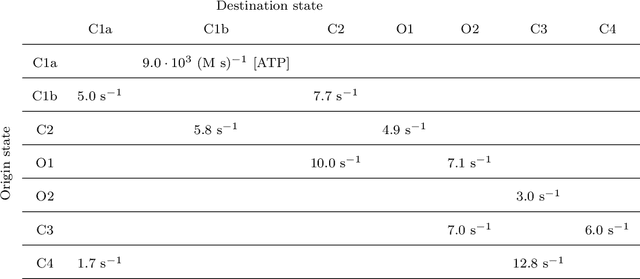
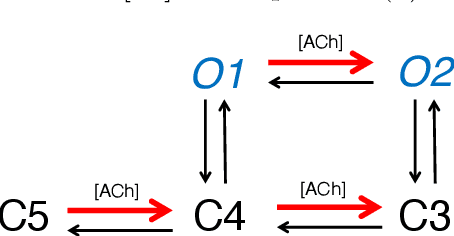
We derive a factor graph EM (FGEM) algorithm, a technique that permits combined parameter estimation and statistical inference, to determine hidden kinetic microstates from patch clamp measurements. Using the cystic fibrosis transmembrane conductance regulator (CFTR) and nicotinic acetylcholine receptor (nAChR) as examples, we perform {\em Monte Carlo} simulations to demonstrate the performance of the algorithm. We show that the performance, measured in terms of the probability of estimation error, approaches the theoretical performance limit of maximum {\em a posteriori} estimation. Moreover, the algorithm provides a reliability score for its estimates, and we demonstrate that the score can be used to further improve the performance of estimation. We use the algorithm to estimate hidden kinetic states in lab-obtained CFTR single channel patch clamp traces.

Control for Multifunctionality: Bioinspired Control Based on Feeding in Aplysia californica

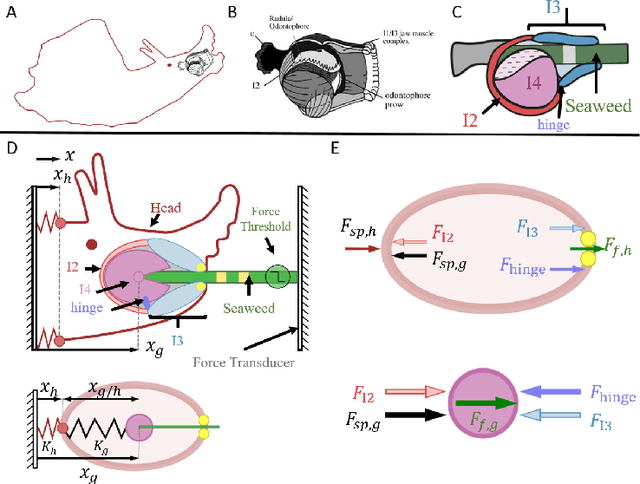
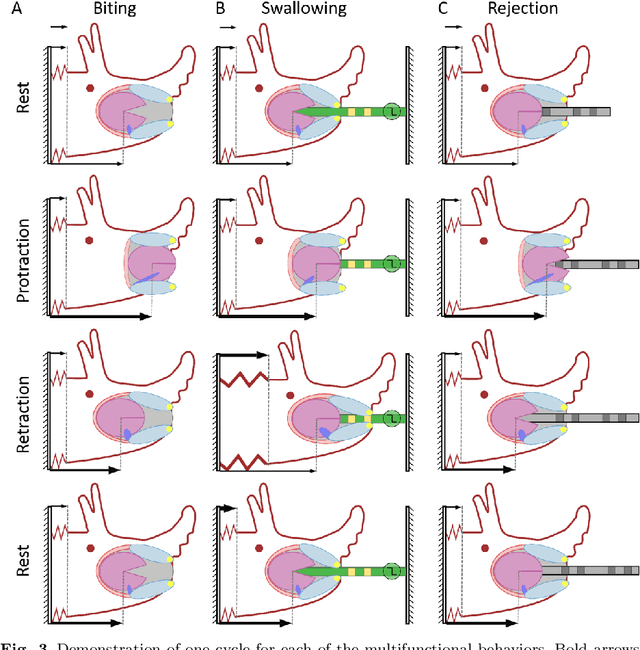
Animals exhibit remarkable feats of behavioral flexibility and multifunctional control that remain challenging for robotic systems. The neural and morphological basis of multifunctionality in animals can provide a source of bio-inspiration for robotic controllers. However, many existing approaches to modeling biological neural networks rely on computationally expensive models and tend to focus solely on the nervous system, often neglecting the biomechanics of the periphery. As a consequence, while these models are excellent tools for neuroscience, they fail to predict functional behavior in real time, which is a critical capability for robotic control. To meet the need for real-time multifunctional control, we have developed a hybrid Boolean model framework capable of modeling neural bursting activity and simple biomechanics at speeds faster than real time. Using this approach, we present a multifunctional model of Aplysia californica feeding that qualitatively reproduces three key feeding behaviors (biting, swallowing, and rejection), demonstrates behavioral switching in response to external sensory cues, and incorporates both known neural connectivity and a simple bioinspired mechanical model of the feeding apparatus. We demonstrate that the model can be used for formulating testable hypotheses and discuss the implications of this approach for robotic control and neuroscience.