A Neural Model for Regular Grammar Induction

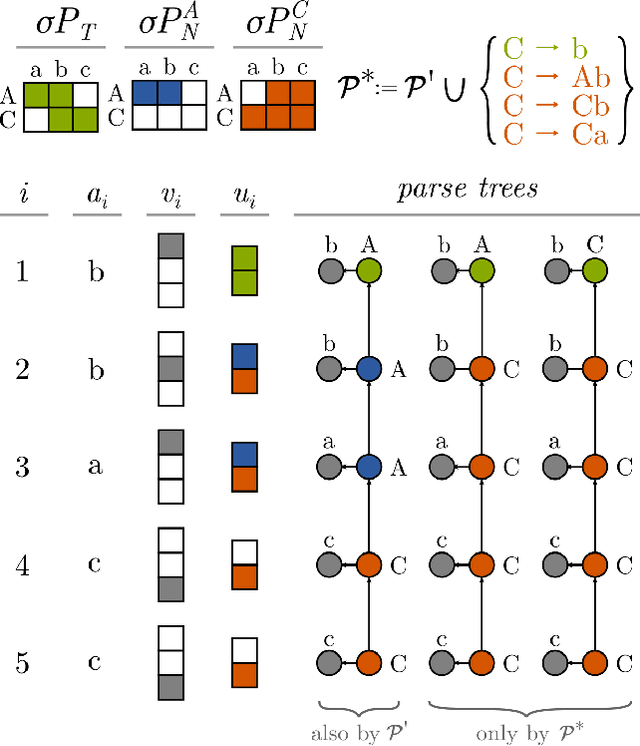
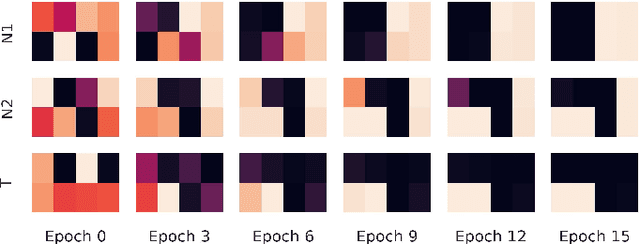
Grammatical inference is a classical problem in computational learning theory and a topic of wider influence in natural language processing. We treat grammars as a model of computation and propose a novel neural approach to induction of regular grammars from positive and negative examples. Our model is fully explainable, its intermediate results are directly interpretable as partial parses, and it can be used to learn arbitrary regular grammars when provided with sufficient data. We find that our method consistently attains high recall and precision scores across a range of tests of varying complexity.

Periodic Extrapolative Generalisation in Neural Networks

The learning of the simplest possible computational pattern -- periodicity -- is an open problem in the research of strong generalisation in neural networks. We formalise the problem of extrapolative generalisation for periodic signals and systematically investigate the generalisation abilities of classical, population-based, and recently proposed periodic architectures on a set of benchmarking tasks. We find that periodic and "snake" activation functions consistently fail at periodic extrapolation, regardless of the trainability of their periodicity parameters. Further, our results show that traditional sequential models still outperform the novel architectures designed specifically for extrapolation, and that these are in turn trumped by population-based training. We make our benchmarking and evaluation toolkit, PerKit, available and easily accessible to facilitate future work in the area.

FACT: Learning Governing Abstractions Behind Integer Sequences

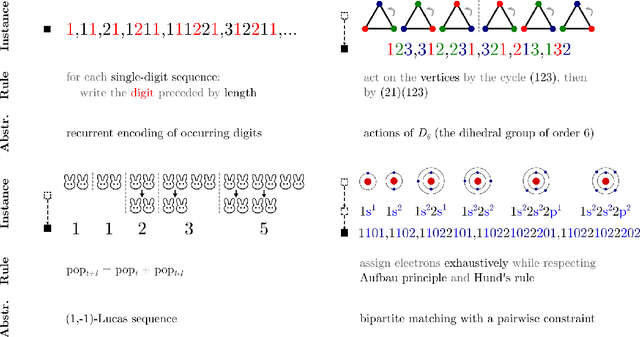
Integer sequences are of central importance to the modeling of concepts admitting complete finitary descriptions. We introduce a novel view on the learning of such concepts and lay down a set of benchmarking tasks aimed at conceptual understanding by machine learning models. These tasks indirectly assess model ability to abstract, and challenge them to reason both interpolatively and extrapolatively from the knowledge gained by observing representative examples. To further aid research in knowledge representation and reasoning, we present FACT, the Finitary Abstraction Comprehension Toolkit. The toolkit surrounds a large dataset of integer sequences comprising both organic and synthetic entries, a library for data pre-processing and generation, a set of model performance evaluation tools, and a collection of baseline model implementations, enabling the making of the future advancements with ease.