Pedro O S Vaz de Melo
Burstiness Scale: a highly parsimonious model for characterizing random series of events
Feb 20, 2016
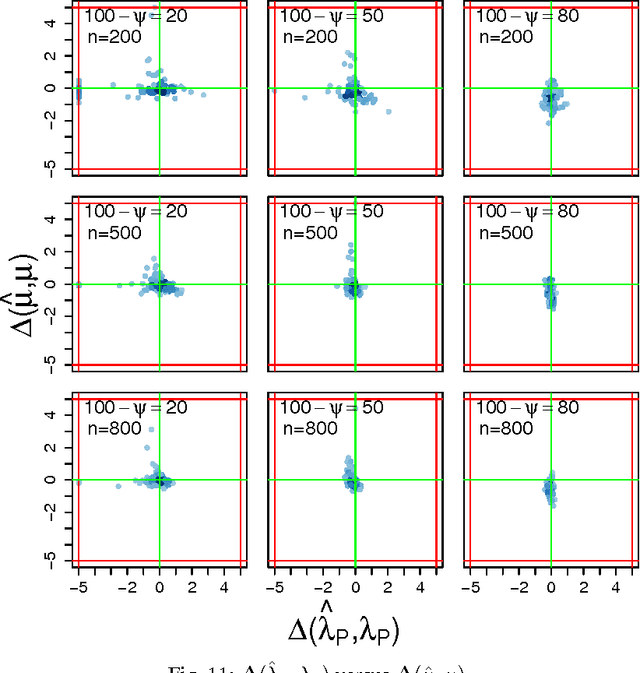
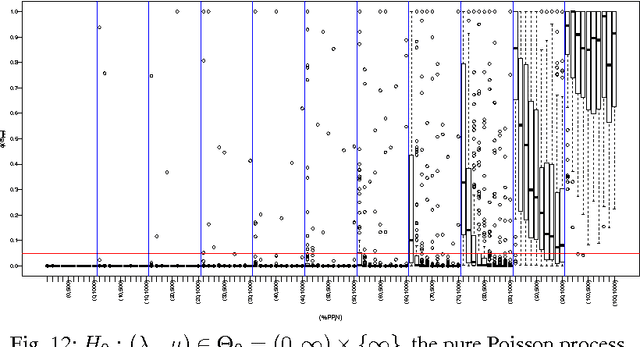
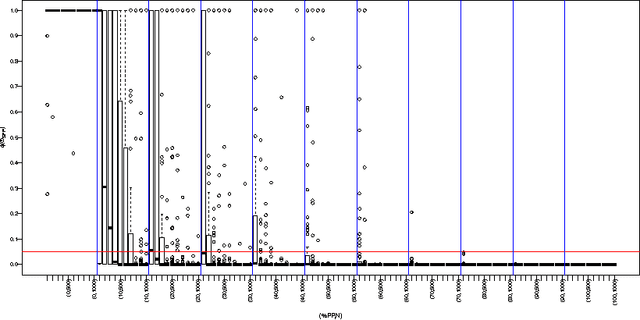
Abstract:The problem to accurately and parsimoniously characterize random series of events (RSEs) present in the Web, such as e-mail conversations or Twitter hashtags, is not trivial. Reports found in the literature reveal two apparent conflicting visions of how RSEs should be modeled. From one side, the Poissonian processes, of which consecutive events follow each other at a relatively regular time and should not be correlated. On the other side, the self-exciting processes, which are able to generate bursts of correlated events and periods of inactivities. The existence of many and sometimes conflicting approaches to model RSEs is a consequence of the unpredictability of the aggregated dynamics of our individual and routine activities, which sometimes show simple patterns, but sometimes results in irregular rising and falling trends. In this paper we propose a highly parsimonious way to characterize general RSEs, namely the Burstiness Scale (BuSca) model. BuSca views each RSE as a mix of two independent process: a Poissonian and a self-exciting one. Here we describe a fast method to extract the two parameters of BuSca that, together, gives the burstyness scale, which represents how much of the RSE is due to bursty and viral effects. We validated our method in eight diverse and large datasets containing real random series of events seen in Twitter, Yelp, e-mail conversations, Digg, and online forums. Results showed that, even using only two parameters, BuSca is able to accurately describe RSEs seen in these diverse systems, what can leverage many applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge