Pavel Záviška
Multiple Hankel matrix rank minimization for audio inpainting
Mar 31, 2023Abstract:Sasaki et al. (2018) presented an efficient audio declipping algorithm, based on the properties of Hankel-structured matrices constructed from time-domain signal blocks. We adapt their approach to solve the audio inpainting problem, where samples are missing in the signal. We analyze the algorithm and provide modifications, some of them leading to an improved performance. Overall, it turns out that the new algorithms perform reasonably well for speech signals but they are not competitive in the case of music signals.
Analysis Social Sparsity Audio Declipper
May 20, 2022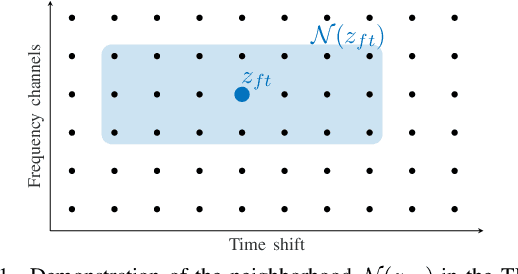
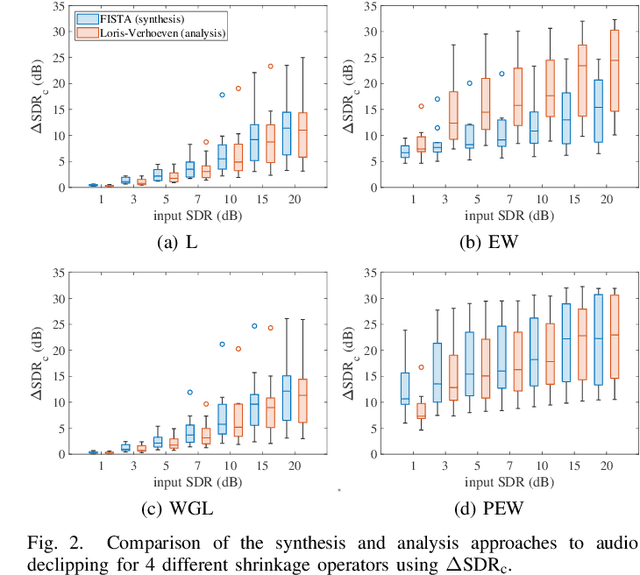
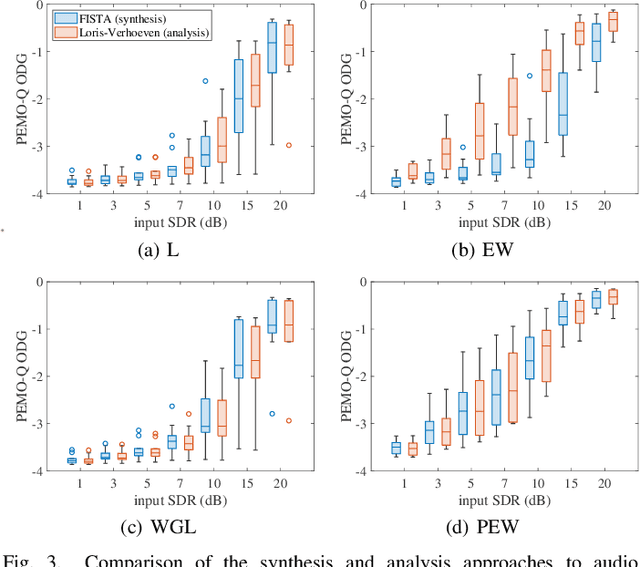
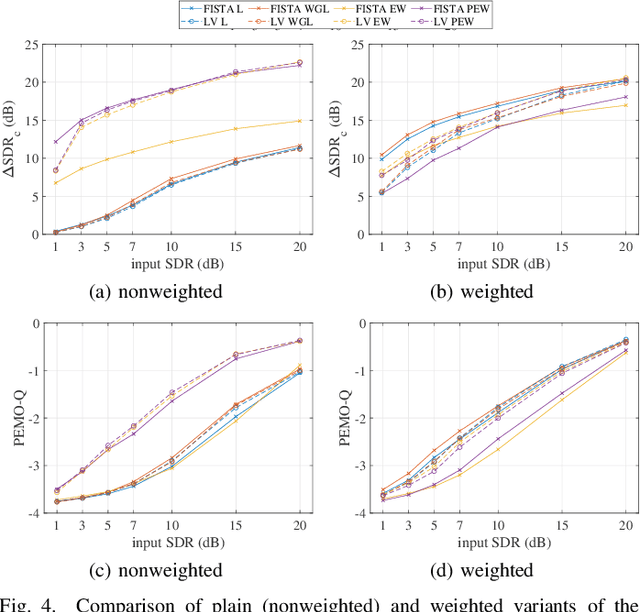
Abstract:We develop the analysis (cosparse) variant of the popular audio declipping algorithm of Siedenburg et al. Furthermore, we extend it by the possibility of weighting the time-frequency coefficients. We examine the audio reconstruction performance of several combinations of weights and shrinkage operators. We show that weights improve the reconstruction quality in some cases; however, the overall scores achieved by the non-weighted are not surpassed. Yet, the analysis Empirical Wiener (EW) shrinkage was able to reach the quality of a computationally more expensive competitor, the Persistent Empirical Wiener (PEW). Moreover, the proposed analysis variant using PEW slightly outperforms the synthesis counterpart in terms of an auditory-motivated metric.
Audio declipping performance enhancement via crossfading
Apr 07, 2021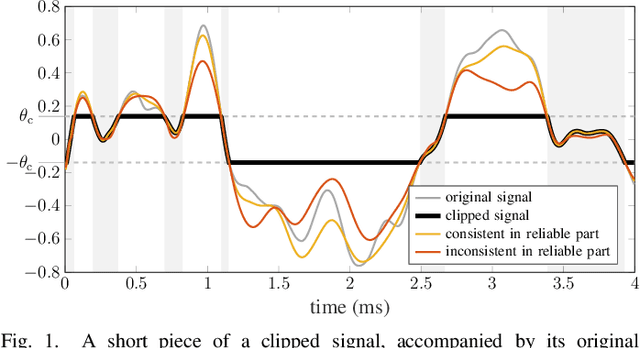
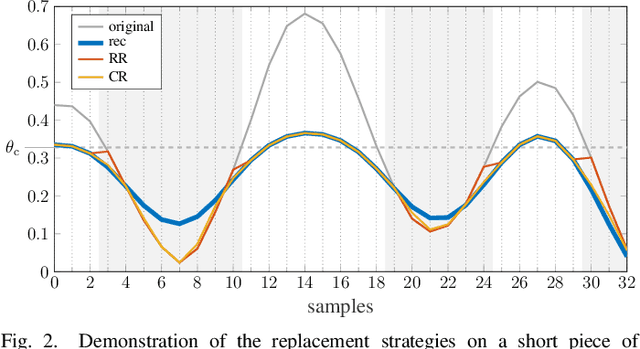
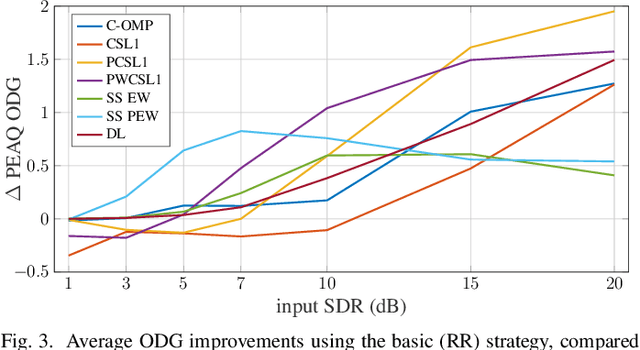
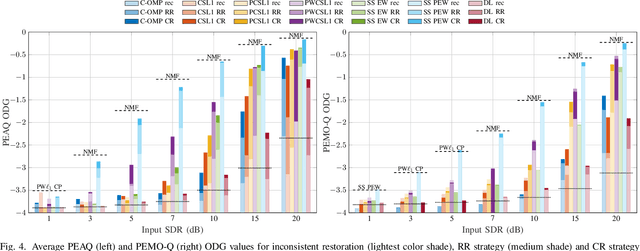
Abstract:Some audio declipping methods produce waveforms that do not fully respect the physical process of clipping, which is why we refer to them as inconsistent. This letter reports what effect on perception it has if the solution by inconsistent methods is forced consistent by postprocessing. We first propose a simple sample replacement method, then we identify its main weaknesses and propose an improved variant. The experiments show that the vast majority of inconsistent declipping methods significantly benefit from the proposed approach in terms of objective perceptual metrics. In particular, we show that the SS PEW method based on social sparsity combined with the proposed method performs comparable to top methods from the consistent class, but at a computational cost of one order of magnitude lower.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge