Patrik Christen
Modelling and Implementing Open-Ended Evolutionary Systems
Jan 18, 2022Abstract:Having a model and being able to implement open-ended evolutionary systems is important for advancing our understanding of open-endedness. Complex systems science and newest generation high-level programming languages provide intriguing possibilities to do so, respectively. Here, some recent advances in modelling and implementing open-ended evolutionary systems are reviewed first. Then, the so-called allagmatic method to describe, model, implement, and interpret complex systems is introduced. After highlighting some current modelling and implementation challenges, model building blocks of open-ended evolutionary systems are identified, a system metamodel of open-ended evolution is formalised in the allagmatic method, and an implementation prototype with a high-level programming language is outlined. The proposed approach shows statistical characteristics of open-ended evolutionary systems and provides a promising starting point to interpret novelty generated at runtime.
Automatic Programming Through Combinatorial Evolution
Feb 20, 2021
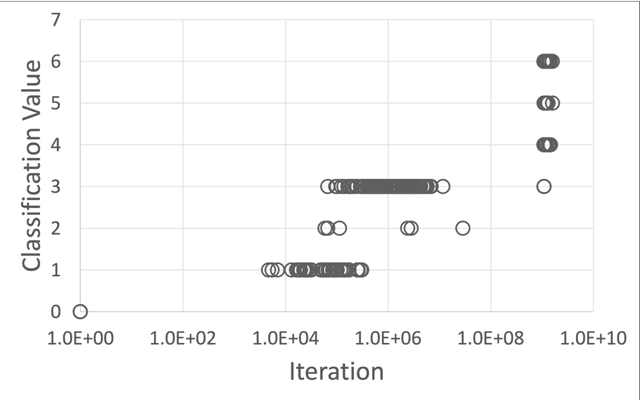

Abstract:It has been already shown that combinatorial evolution - the creation of new things through the combination of existing things - can be a powerful way to evolve rather than design technical objects such as electronic circuits in a computer simulation. Intriguingly, only a few iterations seem to be required to already achieve complex objects. In the present paper we want to employ combinatorial evolution in software development. Our research question is whether it is possible to generate computer programs of increasing complexity using automatic programming through combinatorial evolution. Specifically, we ask what kind of basic code blocks are needed at the beginning, how are these code blocks implemented to allow them to combine, and how can code complexity be measured. We implemented a computer program simulating combinatorial evolution of code blocks stored in a database to make them available for combinations. Automatic programming is achieved by evaluating regular expressions. We found that reserved key words of a programming language are suitable for defining the basic code blocks at the beginning of the simulation. We also found that placeholders can be used to combine code blocks and that code complexity can be described in terms of the importance to the programming language. As in the previous combinatorial evolution simulation of electronic circuits, complexity increased from simple keywords and special characters to more complex variable declarations, to class definitions, to methods, and to classes containing methods and variable declarations. Combinatorial evolution, therefore, seems to be a promising approach for automatic programming.
Adaptation in a System Metamodel for Evolutionary Computation
Aug 31, 2020
Abstract:Complex systems are difficult to model and analyse with traditional mathematics, e.g. analytically solving differential equations. To better understand such systems, we recently presented a system metamodel to provide an algorithmic alternative to analytical methods and were able to create simulations of complex systems modelled as cellular automata and artificial neural networks. In this study we extend our system metamodel with the concept of adaption in order to integrate evolutionary computation in our so-called allagmatic method. Adaption is described in the context of our system metamodel and the allagmatic method, defined and implemented, and computational experiments with cellular automata and artificial neural networks performed. We find that the system metamodel of the allagmatic method integrates adaptation with an additional operation called adaptation function that operates on the update function, which encodes the system's dynamics. It allows the creation of evolutionary computations by providing an abstract template for adaptation and guidance for implementation with the system metamodel. The creation of the system metamodel was first inspired by abstract concepts of the philosophy of individuation of Gilbert Simondon. The theoretical background for the concept of adaptation in this study is taken from the philosophy of organism of Alfred North Whitehead.
System Metamodel Formalism
May 03, 2020
Abstract:Differential equations have been widely and successfully used to describe the macroscopic or global behaviour of systems in general. With inhomogeneous, time-varying, specific, and often non-linear interactions, the dynamics of complex systems is in contrast more efficiently described by local rules and thus in an algorithmic and local or microscopic manner. In order to create computer models of systems, particularly complex systems, we recently presented a so-called allagmatic method including a system metamodel with two concrete implementations of cellular automata and artificial neural networks. Guidance from philosophy and its general concepts were helpful in these first studies focusing on computer modelling and simulation as well as feasibility. A rigorous mathematical formalism of the system metamodel, however, is still missing. This would not only more precisely describe and define the system metamodel, it would also further generalise it and with that extend its reach to formal treatment in applied mathematics and computational mathematics as well as extend its applicability to other mathematical models such as agent-based models. In this study, a mathematical definition of the system metamodel and its model parameters is provided and the creation of concrete mathematical models, i.e. cellular automata and artificial neural networks, from it is proved.
Cybernetical Concepts for Cellular Automaton and Artificial Neural Network Modelling and Implementation
Nov 24, 2019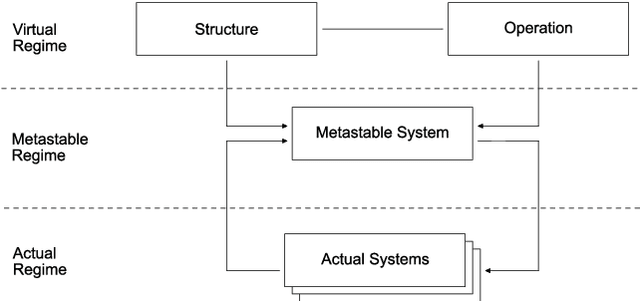
Abstract:As a discipline cybernetics has a long and rich history. In its first generation it not only had a worldwide span, in the area of computer modelling, for example, its proponents such as John von Neumann, Stanislaw Ulam, Warren McCulloch and Walter Pitts, also came up with models and methods such as cellular automata and artificial neural networks, which are still the foundation of most modern modelling approaches. At the same time, cybernetics also got the attention of philosophers, such as the Frenchman Gilbert Simondon, who made use of cybernetical concepts in order to establish a metaphysics and a natural philosophy of individuation, giving cybernetics thereby a philosophical interpretation, which he baptised allagmatic. In this paper, we emphasise this allagmatic theory by showing how Simondon's philosophical concepts can be used to formulate a generic computer model or metamodel for complex systems modelling and its implementation in program code, according to generic programming. We also present how the developed allagmatic metamodel is capable of building simple cellular automata and artificial neural networks.
Automatic Programming of Cellular Automata and Artificial Neural Networks Guided by Philosophy
May 10, 2019
Abstract:Many computer models such as cellular automata have been developed and successfully applied. However, in some cases these models might be restrictive on the possible solutions or their solution is difficult to interpret. To overcome this problem, we outline an approach, the so-called allagmatic method, that automatically creates and programs models with as little limitations as possible but still maintaining human interpretability. We earlier described a meta-model and its building blocks according to the philosophical concepts of structure (spatial dimension) and operation (temporal dimension). They are entity, milieu, and update function that together abstractly describe the meta-model. By automatically combining these building blocks, new models can potentially be created in an evolutionary computation. We propose generic and object-oriented programming to implement the entities and their milieus as dynamic and generic arrays and the update function as a method. We show two experiments where a simple cellular automaton and an artificial neural network are automatically created and programmed. A target state is successfully evolved and learned in the cellular automaton and artificial neural network, respectively. We conclude that the allagmatic method can create and program cellular automaton and artificial neural network models in an automated manner.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge