Towards Fast Coarse-graining and Equation Discovery with Foundation Inference Models

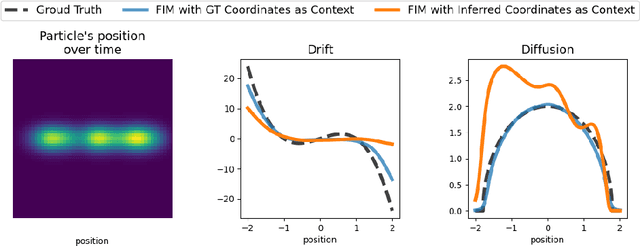
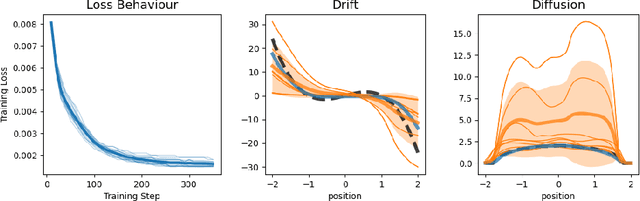
High-dimensional recordings of dynamical processes are often characterized by a much smaller set of effective variables, evolving on low-dimensional manifolds. Identifying these latent dynamics requires solving two intertwined problems: discovering appropriate coarse-grained variables and simultaneously fitting the governing equations. Most machine learning approaches tackle these tasks jointly by training autoencoders together with models that enforce dynamical consistency. We propose to decouple the two problems by leveraging the recently introduced Foundation Inference Models (FIMs). FIMs are pretrained models that estimate the infinitesimal generators of dynamical systems (e.g., the drift and diffusion of a stochastic differential equation) in zero-shot mode. By amortizing the inference of the dynamics through a FIM with frozen weights, and training only the encoder-decoder map, we define a simple, simulation-consistent loss that stabilizes representation learning. A proof of concept on a stochastic double-well system with semicircle diffusion, embedded into synthetic video data, illustrates the potential of this approach for fast and reusable coarse-graining pipelines.

Towards Foundation Inference Models that Learn ODEs In-Context

Ordinary differential equations (ODEs) describe dynamical systems evolving deterministically in continuous time. Accurate data-driven modeling of systems as ODEs, a central problem across the natural sciences, remains challenging, especially if the data is sparse or noisy. We introduce FIM-ODE (Foundation Inference Model for ODEs), a pretrained neural model designed to estimate ODEs zero-shot (i.e., in context) from sparse and noisy observations. Trained on synthetic data, the model utilizes a flexible neural operator for robust ODE inference, even from corrupted data. We empirically verify that FIM-ODE provides accurate estimates, on par with a neural state-of-the-art method, and qualitatively compare the structure of their estimated vector fields.

On Foundation Models for Temporal Point Processes to Accelerate Scientific Discovery

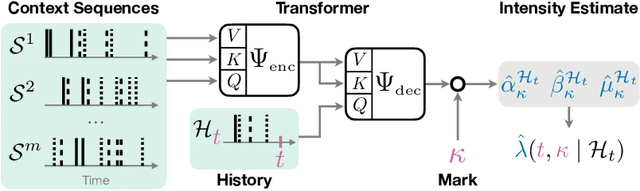
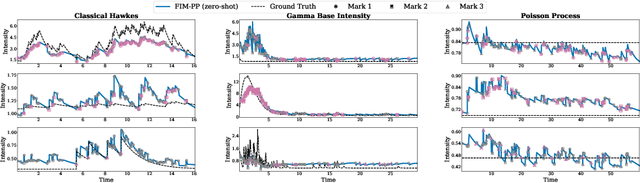
Many scientific fields, from medicine to seismology, rely on analyzing sequences of events over time to understand complex systems. Traditionally, machine learning models must be built and trained from scratch for each new dataset, which is a slow and costly process. We introduce a new approach: a single, powerful model that learns the underlying patterns of event data in context. We trained this "foundation model" on millions of simulated event sequences, teaching it a general-purpose understanding of how events can unfold. As a result, our model can analyze new scientific data instantly, without retraining, simply by looking at a few examples from the dataset. It can also be quickly fine-tuned for even higher accuracy. This approach makes sophisticated event analysis more accessible and accelerates the pace of scientific discovery.

Foundation Inference Models for Stochastic Differential Equations: A Transformer-based Approach for Zero-shot Function Estimation

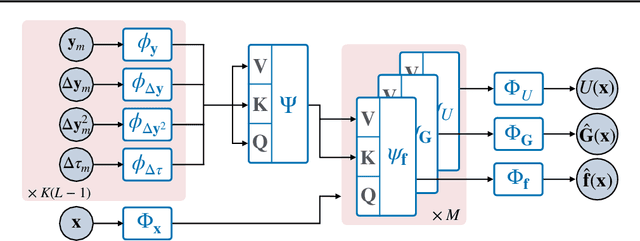
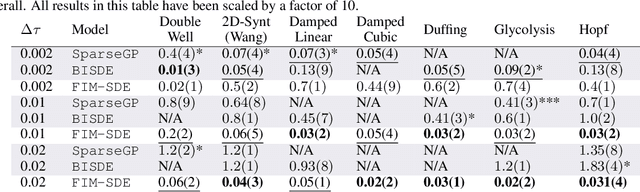
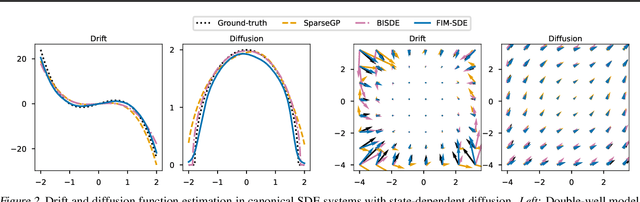
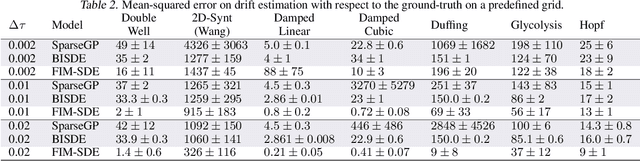
Stochastic differential equations (SDEs) describe dynamical systems where deterministic flows, governed by a drift function, are superimposed with random fluctuations dictated by a diffusion function. The accurate estimation (or discovery) of these functions from data is a central problem in machine learning, with wide application across natural and social sciences alike. Yet current solutions are brittle, and typically rely on symbolic regression or Bayesian non-parametrics. In this work, we introduce FIM-SDE (Foundation Inference Model for SDEs), a transformer-based recognition model capable of performing accurate zero-shot estimation of the drift and diffusion functions of SDEs, from noisy and sparse observations on empirical processes of different dimensionalities. Leveraging concepts from amortized inference and neural operators, we train FIM-SDE in a supervised fashion, to map a large set of noisy and discretely observed SDE paths to their corresponding drift and diffusion functions. We demonstrate that one and the same (pretrained) FIM-SDE achieves robust zero-shot function estimation (i.e. without any parameter fine-tuning) across a wide range of synthetic and real-world processes, from canonical SDE systems (e.g. double-well dynamics or weakly perturbed Hopf bifurcations) to human motion recordings and oil price and wind speed fluctuations.

Foundation Inference Models for Markov Jump Processes

Markov jump processes are continuous-time stochastic processes which describe dynamical systems evolving in discrete state spaces. These processes find wide application in the natural sciences and machine learning, but their inference is known to be far from trivial. In this work we introduce a methodology for zero-shot inference of Markov jump processes (MJPs), on bounded state spaces, from noisy and sparse observations, which consists of two components. First, a broad probability distribution over families of MJPs, as well as over possible observation times and noise mechanisms, with which we simulate a synthetic dataset of hidden MJPs and their noisy observation process. Second, a neural network model that processes subsets of the simulated observations, and that is trained to output the initial condition and rate matrix of the target MJP in a supervised way. We empirically demonstrate that one and the same (pretrained) model can infer, in a zero-shot fashion, hidden MJPs evolving in state spaces of different dimensionalities. Specifically, we infer MJPs which describe (i) discrete flashing ratchet systems, which are a type of Brownian motors, and the conformational dynamics in (ii) molecular simulations, (iii) experimental ion channel data and (iv) simple protein folding models. What is more, we show that our model performs on par with state-of-the-art models which are finetuned to the target datasets.

Foundational Inference Models for Dynamical Systems

Ordinary differential equations (ODEs) underlie dynamical systems which serve as models for a vast number of natural and social phenomena. Yet inferring the ODE that best describes a set of noisy observations on one such phenomenon can be remarkably challenging, and the models available to achieve it tend to be highly specialized and complex too. In this work we propose a novel supervised learning framework for zero-shot inference of ODEs from noisy data. We first generate large datasets of one-dimensional ODEs, by sampling distributions over the space of initial conditions, and the space of vector fields defining them. We then learn neural maps between noisy observations on the solutions of these equations, and their corresponding initial condition and vector fields. The resulting models, which we call foundational inference models (FIM), can be (i) copied and matched along the time dimension to increase their resolution; and (ii) copied and composed to build inference models of any dimensionality, without the need of any finetuning. We use FIM to model both ground-truth dynamical systems of different dimensionalities and empirical time series data in a zero-shot fashion, and outperform state-of-the-art models which are finetuned to these systems. Our (pretrained) FIMs are available online

Neural Markov Jump Processes

Markov jump processes are continuous-time stochastic processes with a wide range of applications in both natural and social sciences. Despite their widespread use, inference in these models is highly non-trivial and typically proceeds via either Monte Carlo or expectation-maximization methods. In this work we introduce an alternative, variational inference algorithm for Markov jump processes which relies on neural ordinary differential equations, and is trainable via back-propagation. Our methodology learns neural, continuous-time representations of the observed data, that are used to approximate the initial distribution and time-dependent transition probability rates of the posterior Markov jump process. The time-independent rates of the prior process are in contrast trained akin to generative adversarial networks. We test our approach on synthetic data sampled from ground-truth Markov jump processes, experimental switching ion channel data and molecular dynamics simulations. Source code to reproduce our experiments is available online.