State-Of-The-Art Algorithms For Low-Rank Dynamic Mode Decomposition

This technical note reviews sate-of-the-art algorithms for linear approximation of high-dimensional dynamical systems using low-rank dynamic mode decomposition (DMD). While repeating several parts of our article "low-rank dynamic mode decomposition: an exact and tractable solution", this work provides additional details useful for building a comprehensive picture of state-of-the-art methods.

Generalized Kernel-Based Dynamic Mode Decomposition

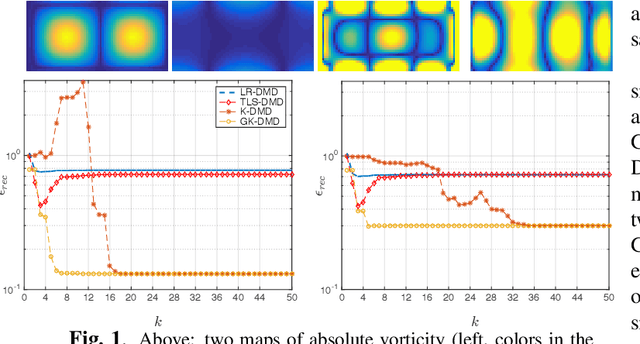
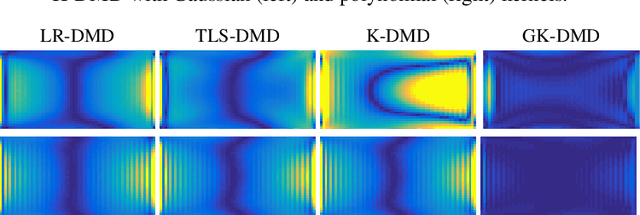
Reduced modeling in high-dimensional reproducing kernel Hilbert spaces offers the opportunity to approximate efficiently non-linear dynamics. In this work, we devise an algorithm based on low rank constraint optimization and kernel-based computation that generalizes a recent approach called "kernel-based dynamic mode decomposition". This new algorithm is characterized by a gain in approximation accuracy, as evidenced by numerical simulations, and in computational complexity.

Low-rank Approximation of Linear Maps

This work provides closed-form solutions and minimal achievable errors for a large class of low-rank approximation problems in Hilbert spaces. The proposed theorem generalizes to the case of linear bounded operators and p-th Schatten norms previous results obtained in the finite dimensional case for the Frobenius norm. The theorem is illustrated in various settings, including low-rank approximation problems with respect to the trace norm, the 2-induced norm or the Hilbert-Schmidt norm. The theorem provides also the basics for the design of tractable algorithms for kernel-based or continuous DMD