Generalized Kernel-Based Dynamic Mode Decomposition
Paper and Code
Feb 11, 2020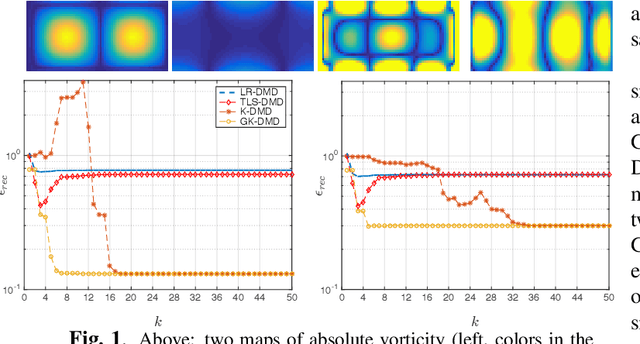
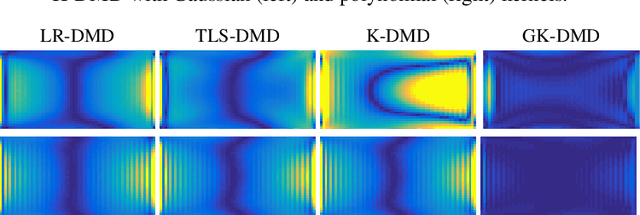
Reduced modeling in high-dimensional reproducing kernel Hilbert spaces offers the opportunity to approximate efficiently non-linear dynamics. In this work, we devise an algorithm based on low rank constraint optimization and kernel-based computation that generalizes a recent approach called "kernel-based dynamic mode decomposition". This new algorithm is characterized by a gain in approximation accuracy, as evidenced by numerical simulations, and in computational complexity.
* 45th International Conference on Acoustics, Speech, and Signal
Processing (ICASSP 2020)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge