Efficient Induction of Language Models Via Probabilistic Concept Formation

This paper presents a novel approach to the acquisition of language models from corpora. The framework builds on Cobweb, an early system for constructing taxonomic hierarchies of probabilistic concepts that used a tabular, attribute-value encoding of training cases and concepts, making it unsuitable for sequential input like language. In response, we explore three new extensions to Cobweb -- the Word, Leaf, and Path variants. These systems encode each training case as an anchor word and surrounding context words, and they store probabilistic descriptions of concepts as distributions over anchor and context information. As in the original Cobweb, a performance element sorts a new instance downward through the hierarchy and uses the final node to predict missing features. Learning is interleaved with performance, updating concept probabilities and hierarchy structure as classification occurs. Thus, the new approaches process training cases in an incremental, online manner that it very different from most methods for statistical language learning. We examine how well the three variants place synonyms together and keep homonyms apart, their ability to recall synonyms as a function of training set size, and their training efficiency. Finally, we discuss related work on incremental learning and directions for further research.

Induction of Selective Bayesian Classifiers

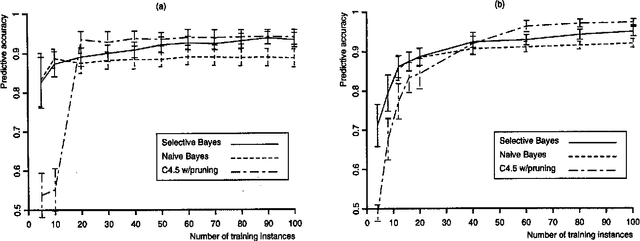
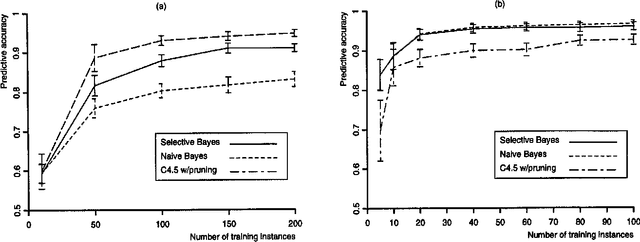
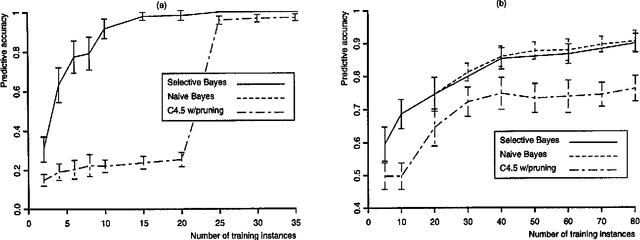
In this paper, we examine previous work on the naive Bayesian classifier and review its limitations, which include a sensitivity to correlated features. We respond to this problem by embedding the naive Bayesian induction scheme within an algorithm that c arries out a greedy search through the space of features. We hypothesize that this approach will improve asymptotic accuracy in domains that involve correlated features without reducing the rate of learning in ones that do not. We report experimental results on six natural domains, including comparisons with decision-tree induction, that support these hypotheses. In closing, we discuss other approaches to extending naive Bayesian classifiers and outline some directions for future research.

Estimating Continuous Distributions in Bayesian Classifiers

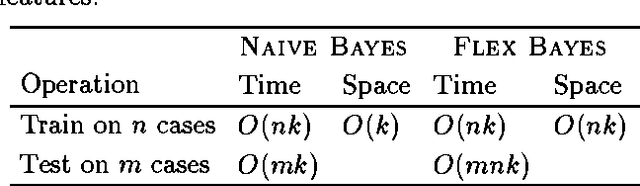
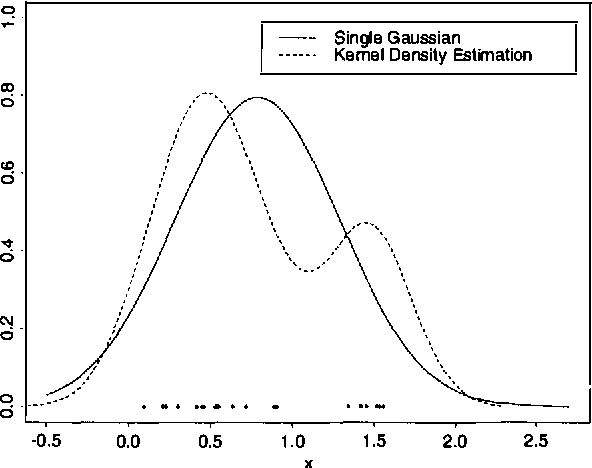
When modeling a probability distribution with a Bayesian network, we are faced with the problem of how to handle continuous variables. Most previous work has either solved the problem by discretizing, or assumed that the data are generated by a single Gaussian. In this paper we abandon the normality assumption and instead use statistical methods for nonparametric density estimation. For a naive Bayesian classifier, we present experimental results on a variety of natural and artificial domains, comparing two methods of density estimation: assuming normality and modeling each conditional distribution with a single Gaussian; and using nonparametric kernel density estimation. We observe large reductions in error on several natural and artificial data sets, which suggests that kernel estimation is a useful tool for learning Bayesian models.