Merging Hazy Sets with m-Schemes: A Geometric Approach to Data Visualization

Many machine learning algorithms try to visualize high dimensional metric data in 2D in such a way that the essential geometric and topological features of the data are highlighted. In this paper, we introduce a framework for aggregating dissimilarity functions that arise from locally adjusting a metric through density-aware normalization, as employed in the IsUMap method. We formalize these approaches as m-schemes, a class of methods closely related to t-norms and t-conorms in probabilistic metrics, as well as to composition laws in information theory. These m-schemes provide a flexible and theoretically grounded approach to refining distance-based embeddings.

IsUMap: Manifold Learning and Data Visualization leveraging Vietoris-Rips filtrations

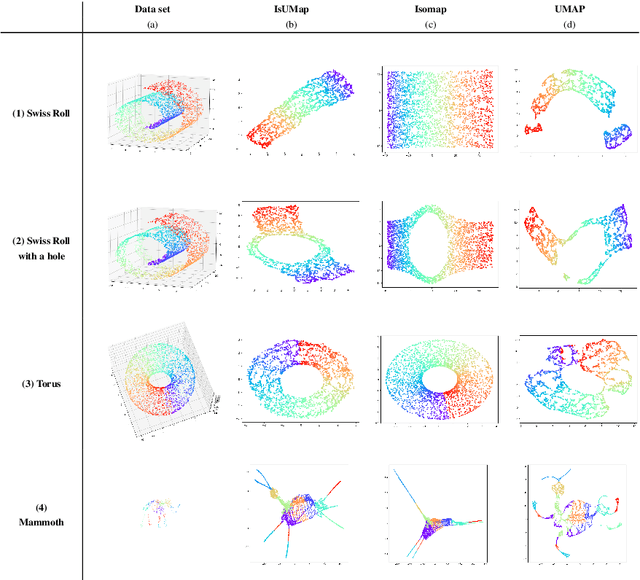
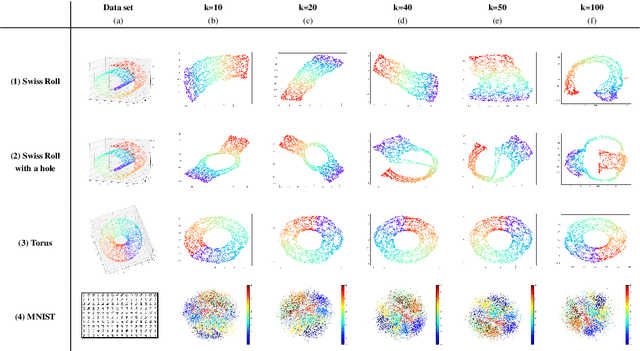
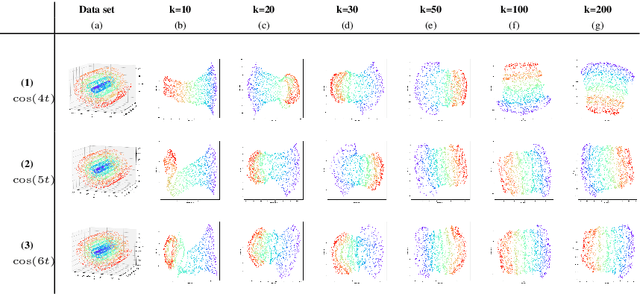
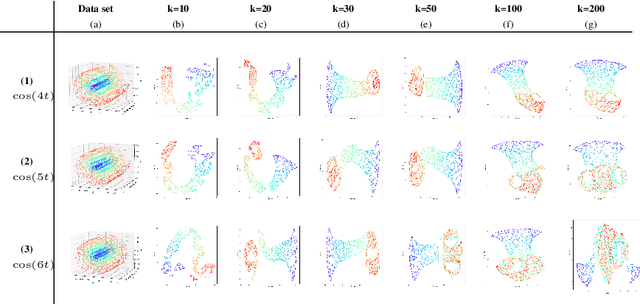
This work introduces IsUMap, a novel manifold learning technique that enhances data representation by integrating aspects of UMAP and Isomap with Vietoris-Rips filtrations. We present a systematic and detailed construction of a metric representation for locally distorted metric spaces that captures complex data structures more accurately than the previous schemes. Our approach addresses limitations in existing methods by accommodating non-uniform data distributions and intricate local geometries. We validate its performance through extensive experiments on examples of various geometric objects and benchmark real-world datasets, demonstrating significant improvements in representation quality.

Geometry of Data

Topological data analysis asks when balls in a metric space $(X,d)$ intersect. Geometric data analysis asks how much balls have to be enlarged to intersect. We connect this principle to the traditional core geometric concept of curvature. This enables us, on one hand, to reconceptualize curvature and link it to the geometric notion of hyperconvexity. On the other hand, we can then also understand methods of topological data analysis from a geometric perspective.