Self-attention in Vision Transformers Performs Perceptual Grouping, Not Attention

Recently, a considerable number of studies in computer vision involves deep neural architectures called vision transformers. Visual processing in these models incorporates computational models that are claimed to implement attention mechanisms. Despite an increasing body of work that attempts to understand the role of attention mechanisms in vision transformers, their effect is largely unknown. Here, we asked if the attention mechanisms in vision transformers exhibit similar effects as those known in human visual attention. To answer this question, we revisited the attention formulation in these models and found that despite the name, computationally, these models perform a special class of relaxation labeling with similarity grouping effects. Additionally, whereas modern experimental findings reveal that human visual attention involves both feed-forward and feedback mechanisms, the purely feed-forward architecture of vision transformers suggests that attention in these models will not have the same effects as those known in humans. To quantify these observations, we evaluated grouping performance in a family of vision transformers. Our results suggest that self-attention modules group figures in the stimuli based on similarity in visual features such as color. Also, in a singleton detection experiment as an instance of saliency detection, we studied if these models exhibit similar effects as those of feed-forward visual salience mechanisms utilized in human visual attention. We found that generally, the transformer-based attention modules assign more salience either to distractors or the ground. Together, our study suggests that the attention mechanisms in vision transformers perform similarity grouping and not attention.

Learning a model of shape selectivity in V4 cells reveals shape encoding mechanisms in the brain

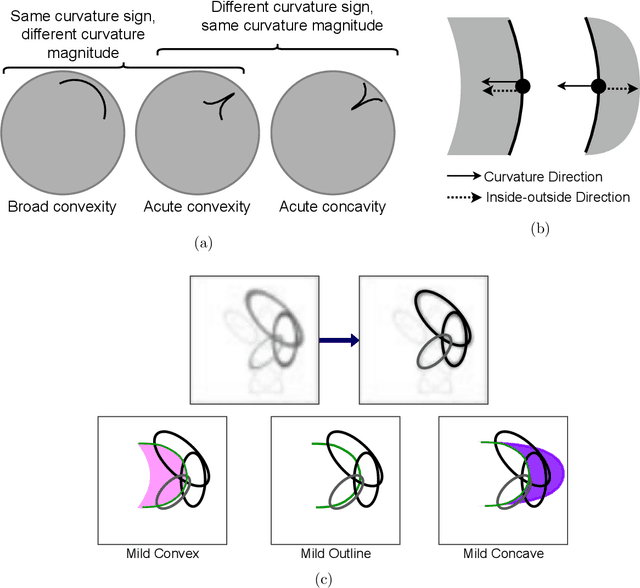
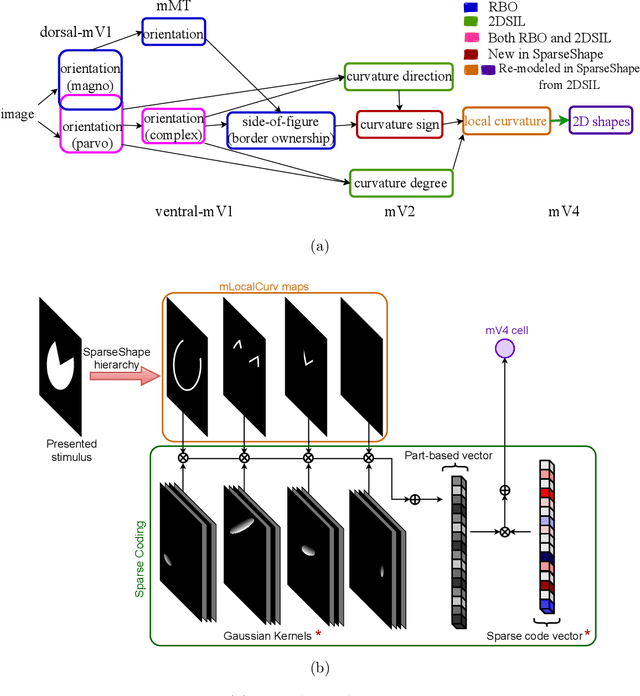
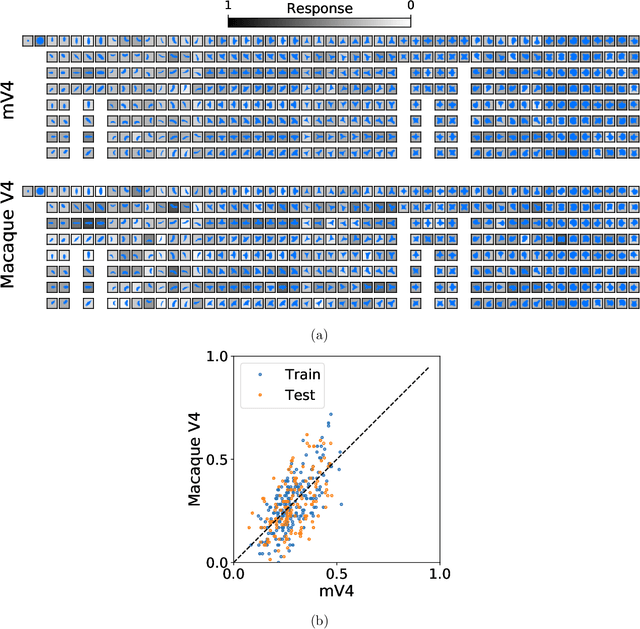
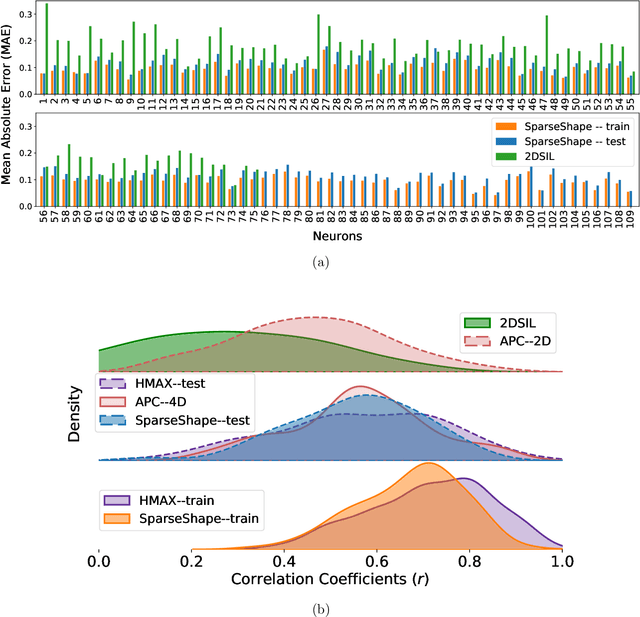
The mechanisms involved in transforming early visual signals to curvature representations in V4 are unknown. We propose a hierarchical model that reveals V1/V2 encodings that are essential components for this transformation to the reported curvature representations in V4. Then, by relaxing the often-imposed prior of a single Gaussian, V4 shape selectivity is learned in the last layer of the hierarchy from Macaque V4 responses. We found that V4 cells integrate multiple shape parts from the full spatial extent of their receptive fields with similar excitatory and inhibitory contributions. Our results uncover new details in existing data about shape selectivity in V4 neurons that with further experiments can enhance our understanding of processing in this area. Accordingly, we propose designs for a stimulus set that allow removing shape parts without disturbing the curvature signal to isolate part contributions to V4 responses.

Multiplicative modulations in hue-selective cells enhance unique hue representation

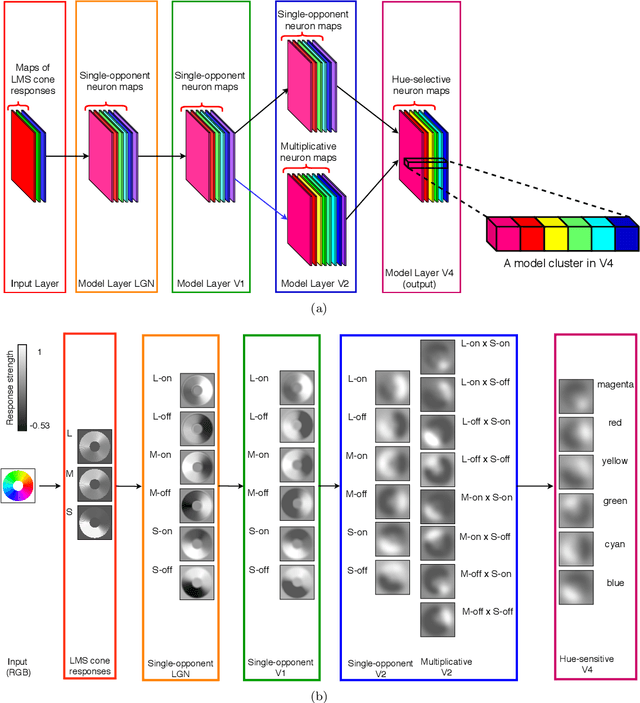
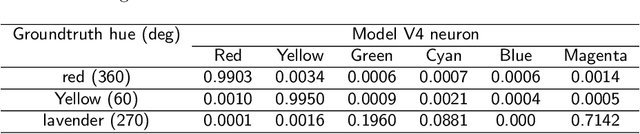
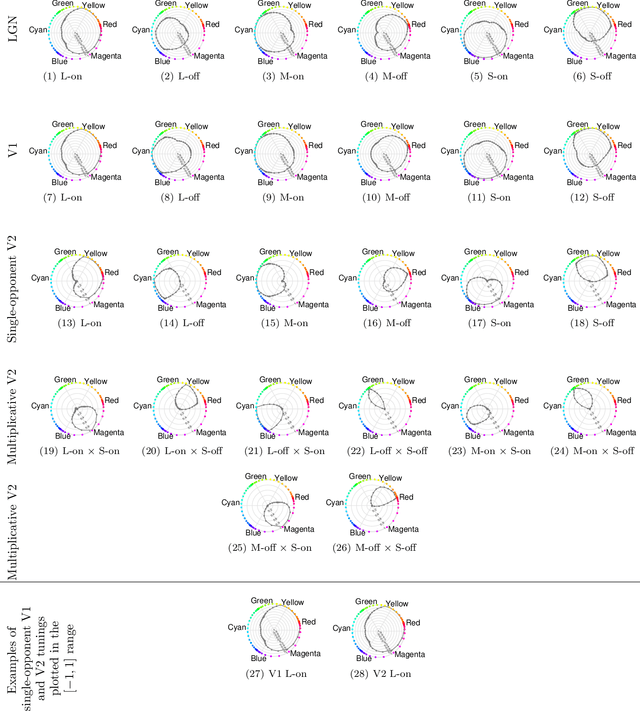
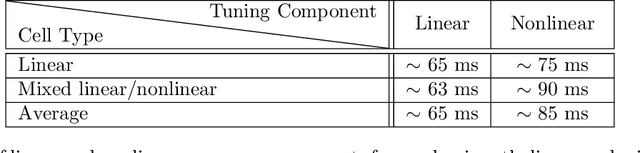
There is still much to understand about the color processing mechanisms in the brain and the transformation from cone-opponent representations to perceptual hues. Moreover, it is unclear which areas(s) in the brain represent unique hues. We propose a hierarchical model inspired by the neuronal mechanisms in the brain for local hue representation, which reveals the contributions of each visual cortical area in hue representation. Local hue encoding is achieved through incrementally increasing processing nonlinearities beginning with cone input. Besides employing nonlinear rectifications, we propose multiplicative modulations as a form of nonlinearity. Our simulation results indicate that multiplicative modulations have significant contributions in encoding of hues along intermediate directions in the MacLeod-Boynton diagram and that model V4 neurons have the capacity to encode unique hues. Additionally, responses of our model neurons resemble those of biological color cells, suggesting that our model provides a novel formulation of the brain's color processing pathway.

Early recurrence enables figure border ownership

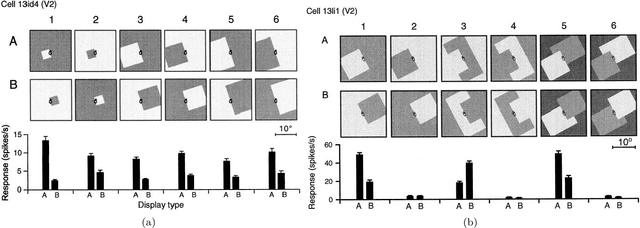
The face-vase illusion introduced by Rubin demonstrates how one can switch back and forth between two different interpretations depending on how the figure outlines are assigned [1]. This border ownership assignment is an important step in the perception of forms. Zhou et al. [2] found neurons in the visual cortex whose responses not only depend on the local features present in their classical receptive fields, but also on their contextual information. Various models proposed that feedback from higher ventral areas or lateral connections could provide the required contextual information. However, some studies [3, 4, 5] ruled out the plausibility of models exclusively based on lateral connections. In addition, further evidence [6] suggests that ventral feedback even from V4 is not fast enough to provide context to border ownership neurons in either V1 or V2. As a result, the border ownership assignment mechanism in the brain is a mystery yet to be solved. Here, we test with computational simulations the hypothesis that the dorsal stream provides the global information to border ownership cells in the ventral stream. Our proposed model incorporates early recurrence from the dorsal pathway as well as lateral modulations within the ventral stream. Our simulation experiments show that our model border ownership neurons, similar to their biological counterparts, exhibit different responses to figures on either side of the border.

Color-opponent mechanisms for local hue encoding in a hierarchical framework

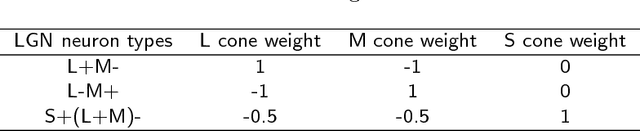
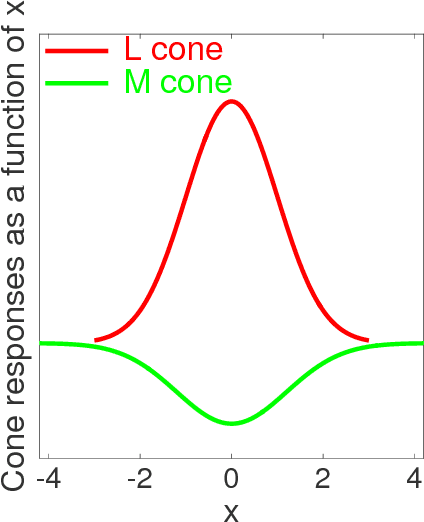
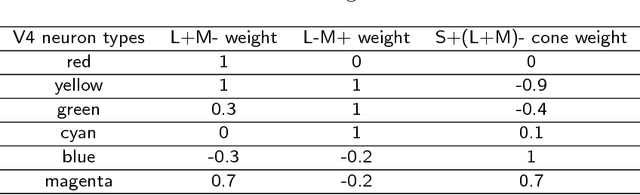
A biologically plausible computational model for color representation is introduced. We present a mechanistic hierarchical model of neurons that not only successfully encodes local hue, but also explicitly reveals how the contributions of each visual cortical layer participating in the process can lead to a hue representation. Our proposed model benefits from studies on the visual cortex and builds a network of single-opponent and hue-selective neurons. Local hue encoding is achieved through gradually increasing nonlinearity in terms of cone inputs to single-opponent cells. We demonstrate that our model's single-opponent neurons have wide tuning curves, while the hue-selective neurons in our model V4 layer exhibit narrower tunings, resembling those in V4 of the primate visual system. Our simulation experiments suggest that neurons in V4 or later layers have the capacity of encoding unique hues. Moreover, with a few examples, we present the possibility of spanning the infinite space of physical hues by combining the hue-selective neurons in our model.