Traffic estimation in unobserved network locations using data-driven macroscopic models

This paper leverages macroscopic models and multi-source spatiotemporal data collected from automatic traffic counters and probe vehicles to accurately estimate traffic flow and travel time in links where these measurements are unavailable. This problem is critical in transportation planning applications where the sensor coverage is low and the planned interventions have network-wide impacts. The proposed model, named the Macroscopic Traffic Estimator (MaTE), can perform network-wide estimations of traffic flow and travel time only using the set of observed measurements of these quantities. Because MaTE is grounded in macroscopic flow theory, all parameters and variables are interpretable. The estimated traffic flow satisfies fundamental flow conservation constraints and exhibits an increasing monotonic relationship with the estimated travel time. Using logit-based stochastic traffic assignment as the principle for routing flow behavior makes the model fully differentiable with respect to the model parameters. This property facilitates the application of computational graphs to learn parameters from vast amounts of spatiotemporal data. We also integrate neural networks and polynomial kernel functions to capture link flow interactions and enrich the mapping of traffic flows into travel times. MaTE also adds a destination choice model and a trip generation model that uses historical data on the number of trips generated by location. Experiments on synthetic data show that the model can accurately estimate travel time and traffic flow in out-of-sample links. Results obtained using real-world multi-source data from a large-scale transportation network suggest that MaTE outperforms data-driven benchmarks, especially in travel time estimation. The estimated parameters of MaTE are also informative about the hourly change in travel demand and supply characteristics of the transportation network.

Statistical inference of travelers' route choice preferences with system-level data

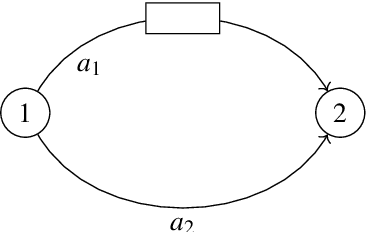
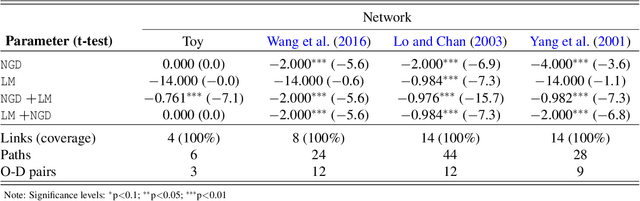
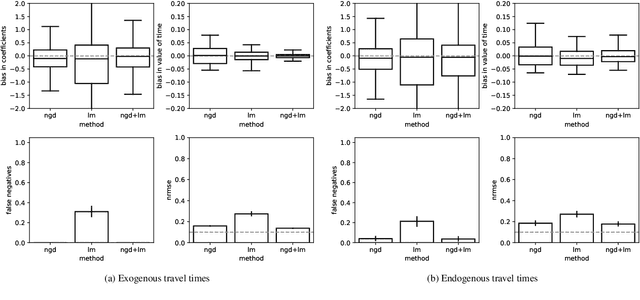
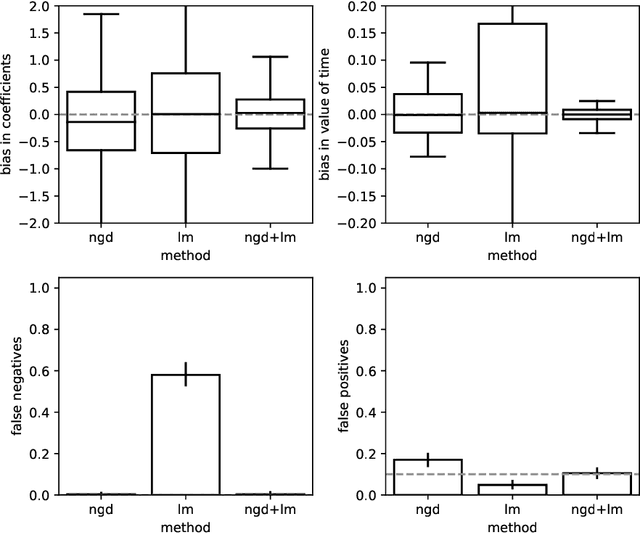
Traditional network models encapsulate travel behavior among all origin-destination pairs based on a simplified and generic utility function. Typically, the utility function consists of travel time solely and its coefficients are equated to estimates obtained from stated preference data. While this modeling strategy is reasonable, the inherent sampling bias in individual-level data may be further amplified over network flow aggregation, leading to inaccurate flow estimates. This data must be collected from surveys or travel diaries, which may be labor intensive, costly and limited to a small time period. To address these limitations, this study extends classical bi-level formulations to estimate travelers' utility functions with multiple attributes using system-level data. We formulate a methodology grounded on non-linear least squares to statistically infer travelers' utility function in the network context using traffic counts, traffic speeds, traffic incidents and sociodemographic information, among other attributes. The analysis of the mathematical properties of the optimization problem and of its pseudo-convexity motivate the use of normalized gradient descent. We also develop a hypothesis test framework to examine statistical properties of the utility function coefficients and to perform attributes selection. Experiments on synthetic data show that the coefficients are consistently recovered and that hypothesis tests are a reliable statistic to identify which attributes are determinants of travelers' route choices. Besides, a series of Monte-Carlo experiments suggest that statistical inference is robust to noise in the Origin-Destination matrix and in the traffic counts, and to various levels of sensor coverage. The methodology is also deployed at a large scale using real-world multi-source data in Fresno, CA collected before and during the COVID-19 outbreak.