Comparison of Point Process Learning and its special case Takacs-Fiksel estimation

Recently, Cronie et al. (2024) introduced the notion of cross-validation for point processes and a new statistical methodology called Point Process Learning (PPL). In PPL one splits a point process/pattern into a training and a validation set, and then predicts the latter from the former through a parametrised Papangelou conditional intensity. The model parameters are estimated by minimizing a point process prediction error; this notion was introduced as the second building block of PPL. It was shown that PPL outperforms the state-of-the-art in both kernel intensity estimation and estimation of the parameters of the Gibbs hard-core process. In the latter case, the state-of-the-art was represented by pseudolikelihood estimation. In this paper we study PPL in relation to Takacs-Fiksel estimation, of which pseudolikelihood is a special case. We show that Takacs-Fiksel estimation is a special case of PPL in the sense that PPL with a specific loss function asymptotically reduces to Takacs-Fiksel estimation if we let the cross-validation regime tend to leave-one-out cross-validation. Moreover, PPL involves a certain type of hyperparameter given by a weight function which ensures that the prediction errors have expectation zero if and only if we have the correct parametrisation. We show that the weight function takes an explicit but intractable form for general Gibbs models. Consequently, we propose different approaches to estimate the weight function in practice. In order to assess how the general PPL setup performs in relation to its special case Takacs-Fiksel estimation, we conduct a simulation study where we find that for common Gibbs models we can find loss functions and hyperparameters so that PPL typically outperforms Takacs-Fiksel estimation significantly in terms of mean square error. Here, the hyperparameters are the cross-validation parameters and the weight function estimate.

Statistical learning and cross-validation for point processes

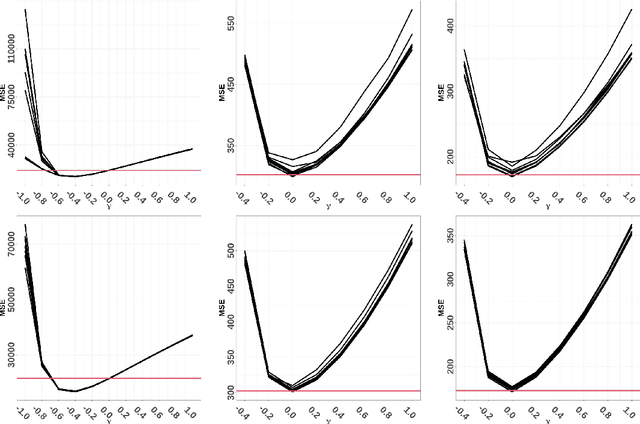
This paper presents the first general (supervised) statistical learning framework for point processes in general spaces. Our approach is based on the combination of two new concepts, which we define in the paper: i) bivariate innovations, which are measures of discrepancy/prediction-accuracy between two point processes, and ii) point process cross-validation (CV), which we here define through point process thinning. The general idea is to carry out the fitting by predicting CV-generated validation sets using the corresponding training sets; the prediction error, which we minimise, is measured by means of bivariate innovations. Having established various theoretical properties of our bivariate innovations, we study in detail the case where the CV procedure is obtained through independent thinning and we apply our statistical learning methodology to three typical spatial statistical settings, namely parametric intensity estimation, non-parametric intensity estimation and Papangelou conditional intensity fitting. Aside from deriving theoretical properties related to these cases, in each of them we numerically show that our statistical learning approach outperforms the state of the art in terms of mean (integrated) squared error.