Classification and Verification of Online Handwritten Signatures with Time Causal Information Theory Quantifiers

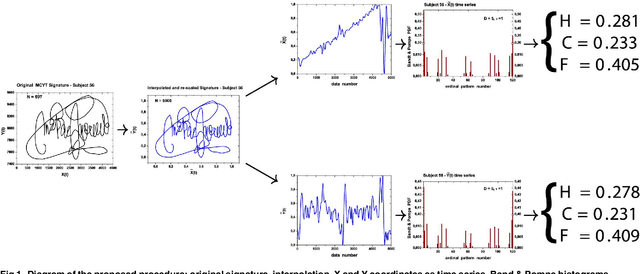
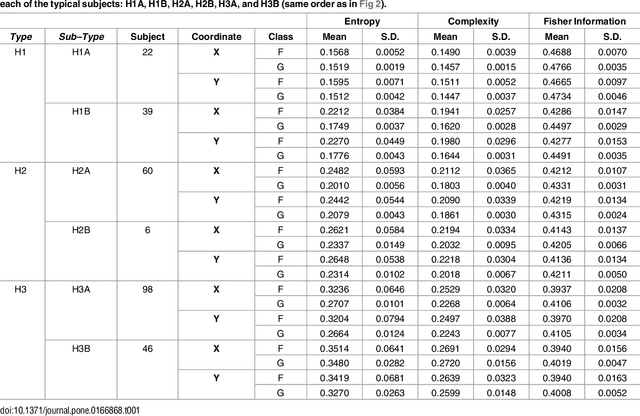
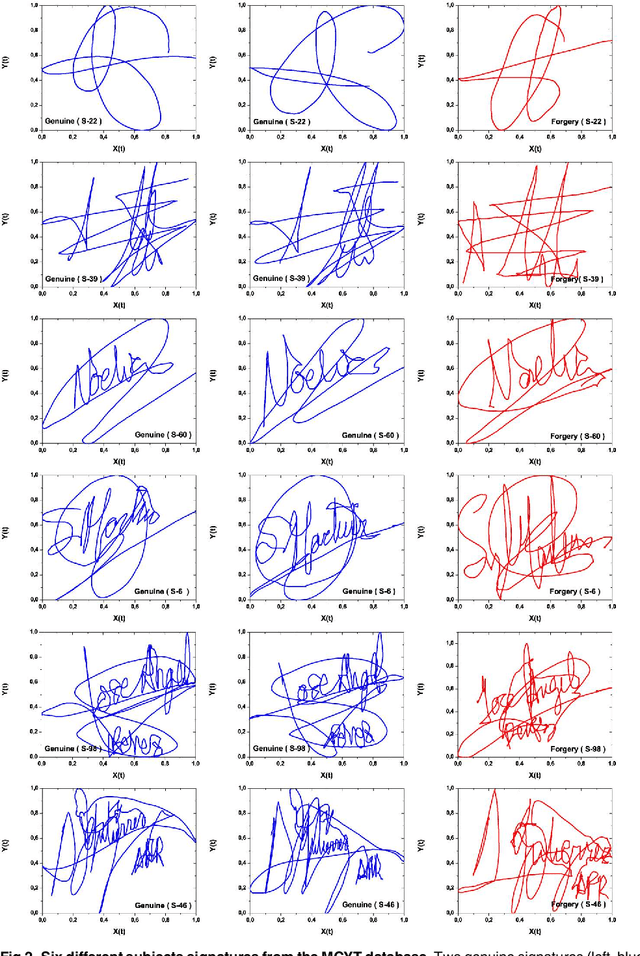
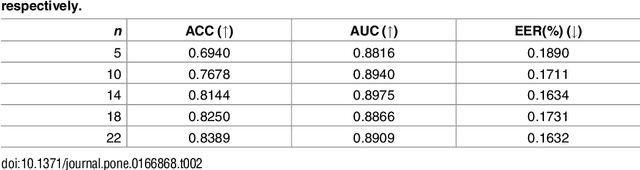
We present a new approach for online handwritten signature classification and verification based on descriptors stemming from Information Theory. The proposal uses the Shannon Entropy, the Statistical Complexity, and the Fisher Information evaluated over the Bandt and Pompe symbolization of the horizontal and vertical coordinates of signatures. These six features are easy and fast to compute, and they are the input to an One-Class Support Vector Machine classifier. The results produced surpass state-of-the-art techniques that employ higher-dimensional feature spaces which often require specialized software and hardware. We assess the consistency of our proposal with respect to the size of the training sample, and we also use it to classify the signatures into meaningful groups.

Distinguishing noise from chaos: objective versus subjective criteria using Horizontal Visibility Graph

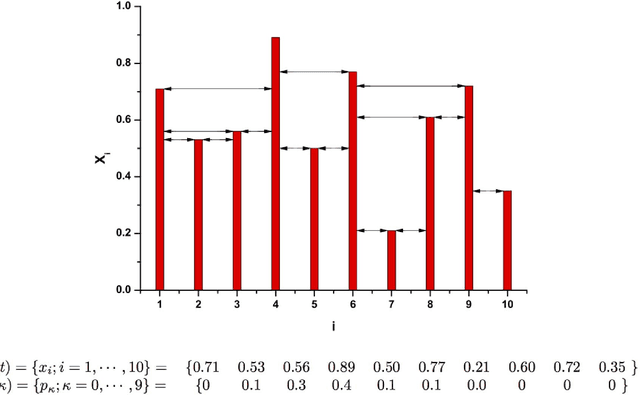
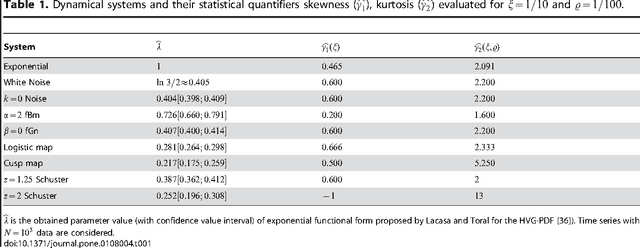
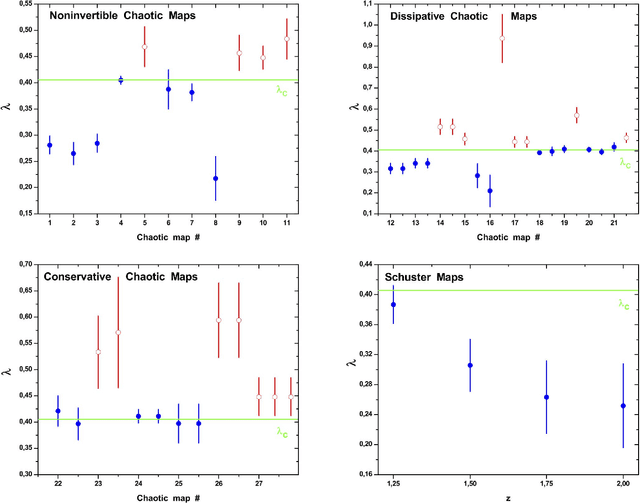
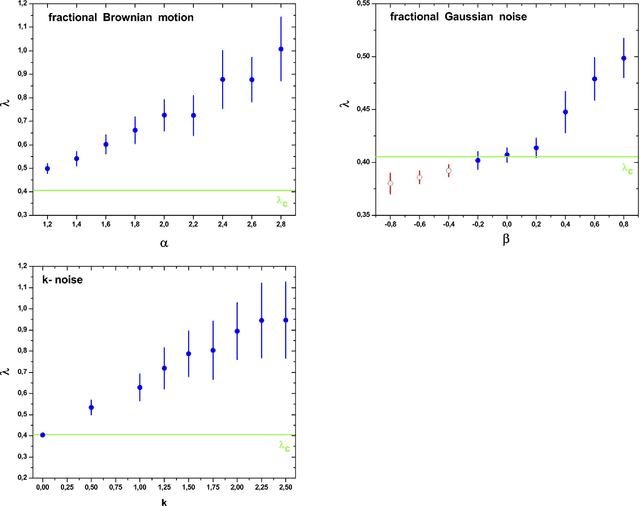
A recently proposed methodology called the Horizontal Visibility Graph (HVG) [Luque {\it et al.}, Phys. Rev. E., 80, 046103 (2009)] that constitutes a geometrical simplification of the well known Visibility Graph algorithm [Lacasa {\it et al.\/}, Proc. Natl. Sci. U.S.A. 105, 4972 (2008)], has been used to study the distinction between deterministic and stochastic components in time series [L. Lacasa and R. Toral, Phys. Rev. E., 82, 036120 (2010)]. Specifically, the authors propose that the node degree distribution of these processes follows an exponential functional of the form $P(\kappa)\sim \exp(-\lambda~\kappa)$, in which $\kappa$ is the node degree and $\lambda$ is a positive parameter able to distinguish between deterministic (chaotic) and stochastic (uncorrelated and correlated) dynamics. In this work, we investigate the characteristics of the node degree distributions constructed by using HVG, for time series corresponding to $28$ chaotic maps and $3$ different stochastic processes. We thoroughly study the methodology proposed by Lacasa and Toral finding several cases for which their hypothesis is not valid. We propose a methodology that uses the HVG together with Information Theory quantifiers. An extensive and careful analysis of the node degree distributions obtained by applying HVG allow us to conclude that the Fisher-Shannon information plane is a remarkable tool able to graphically represent the different nature, deterministic or stochastic, of the systems under study.

Generalized Statistical Complexity of SAR Imagery

A new generalized Statistical Complexity Measure (SCM) was proposed by Rosso et al in 2010. It is a functional that captures the notions of order/disorder and of distance to an equilibrium distribution. The former is computed by a measure of entropy, while the latter depends on the definition of a stochastic divergence. When the scene is illuminated by coherent radiation, image data is corrupted by speckle noise, as is the case of ultrasound-B, sonar, laser and Synthetic Aperture Radar (SAR) sensors. In the amplitude and intensity formats, this noise is multiplicative and non-Gaussian requiring, thus, specialized techniques for image processing and understanding. One of the most successful family of models for describing these images is the Multiplicative Model which leads, among other probability distributions, to the G0 law. This distribution has been validated in the literature as an expressive and tractable model, deserving the "universal" denomination for its ability to describe most types of targets. In order to compute the statistical complexity of a site in an image corrupted by speckle noise, we assume that the equilibrium distribution is that of fully developed speckle, namely the Gamma law in intensity format, which appears in areas with little or no texture. We use the Shannon entropy along with the Hellinger distance to measure the statistical complexity of intensity SAR images, and we show that it is an expressive feature capable of identifying many types of targets.