Fine-tuning Vision Transformers for the Prediction of State Variables in Ising Models

Transformers are state-of-the-art deep learning models that are composed of stacked attention and point-wise, fully connected layers designed for handling sequential data. Transformers are not only ubiquitous throughout Natural Language Processing (NLP), but, recently, they have inspired a new wave of Computer Vision (CV) applications research. In this work, a Vision Transformer (ViT) is applied to predict the state variables of 2-dimensional Ising model simulations. Our experiments show that ViT outperform state-of-the-art Convolutional Neural Networks (CNN) when using a small number of microstate images from the Ising model corresponding to various boundary conditions and temperatures. This work opens the possibility of applying ViT to other simulations, and raises interesting research directions on how attention maps can learn about the underlying physics governing different phenomena.

Application of the Quantum Potential Neural Network to multi-electronic atoms

In this report, the application of the Quantum Potential Neural Network (QPNN) framework to many electron atomic systems is presented. For this study, full configuration interaction (FCI) one--electron density functions within predefined limits of accuracy were used to train the QPNN. The obtained results suggest that this new neural network is capable of learning the effective potential functions of many electron atoms in a completely unsupervised manner, and using only limited information from the probability density. Using the effective potential functions learned for each of the studied systems the QPNN was able to estimate the total energies of each of the systems (with a maximum of 10 trials) with a remarkable accuracy when compared to the FCI energies.

Learning Potentials of Quantum Systems using Deep Neural Networks

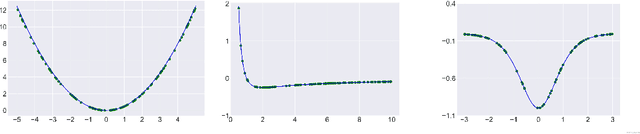
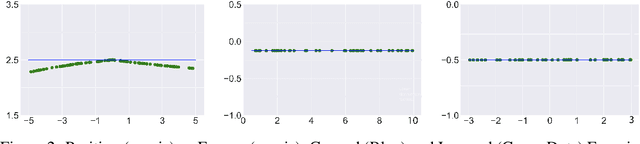
Machine Learning has wide applications in a broad range of subjects, including physics. Recent works have shown that neural networks can learn classical Hamiltonian mechanics. The results of these works motivate the following question: Can we endow neural networks with inductive biases coming from quantum mechanics and provide insights for quantum phenomena? In this work, we try answering these questions by investigating possible approximations for reconstructing the Hamiltonian of a quantum system given one of its wave--functions. Instead of handcrafting the Hamiltonian and a solution of the Schr\"odinger equation, we design neural networks that aim to learn it directly from our observations. We show that our method, termed Quantum Potential Neural Networks (QPNN), can learn potentials in an unsupervised manner with remarkable accuracy for a wide range of quantum systems, such as the quantum harmonic oscillator, particle in a box perturbed by an external potential, hydrogen atom, P\"oschl--Teller potential, and a solitary wave system. Furthermore, in the case of a particle perturbed by an external force, we also learn the perturbed wave function in a joint end-to-end manner.