Onit Alalouf
Diffractive optical system design by cascaded propagation
Feb 23, 2022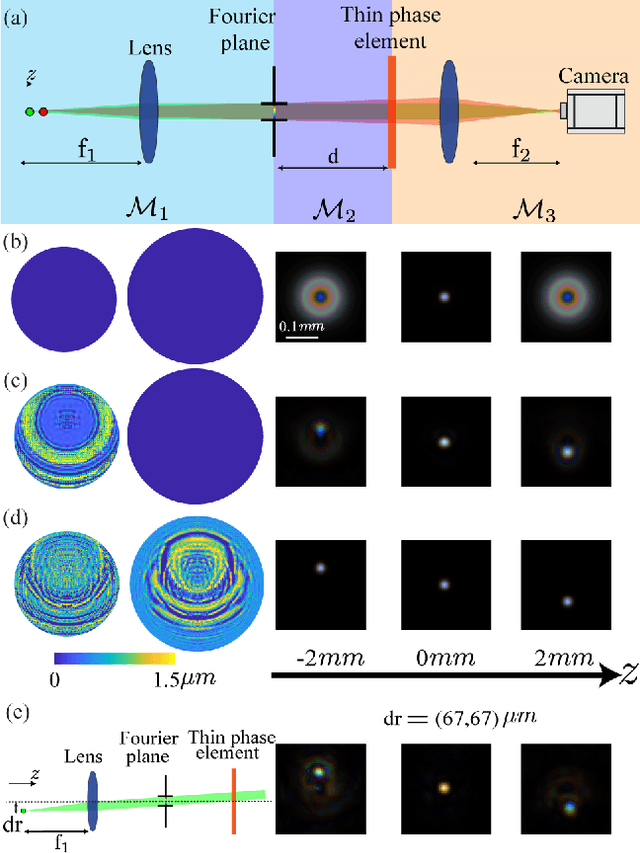

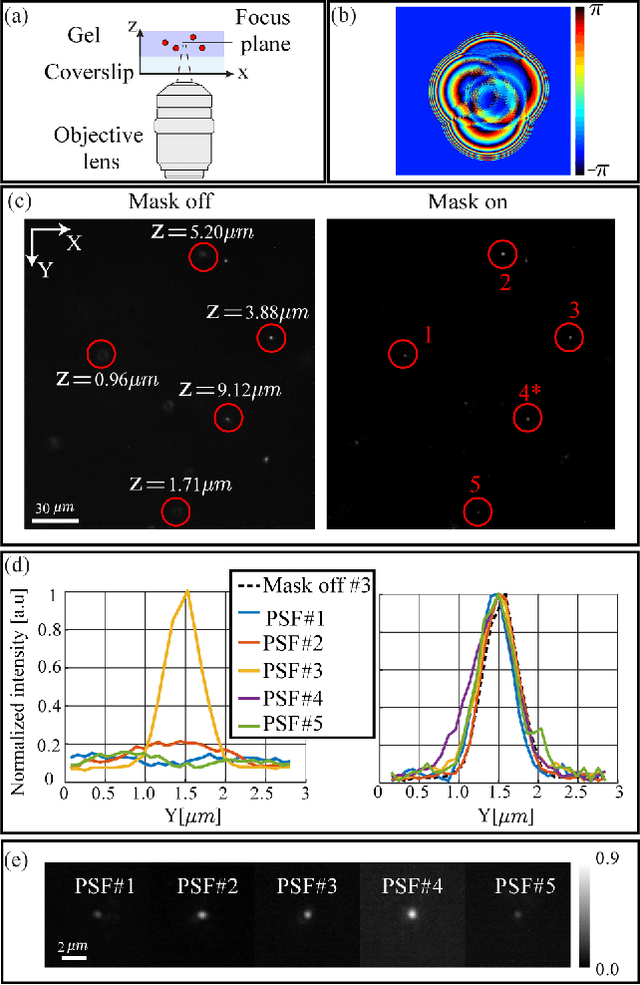
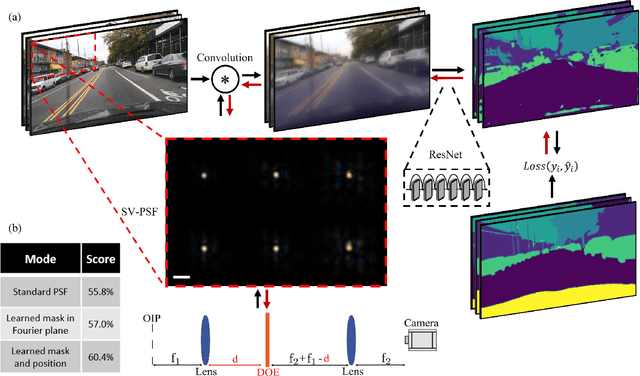
Abstract:Modern design of complex optical systems relies heavily on computational tools. These typically utilize geometrical optics as well as Fourier optics, which enables the use of diffractive elements to manipulate light with features on the scale of a wavelength. Fourier optics is typically used for designing thin elements, placed in the system's aperture, generating a shift-invariant Point Spread Function (PSF). A major bottleneck in applying Fourier Optics in many cases of interest, e.g. when dealing with multiple, or out-of-aperture elements, comes from numerical complexity. In this work, we propose and implement an efficient and differentiable propagation model based on the Collins integral, which enables the optimization of diffraction optical systems with unprecedented design freedom using backpropagation. We demonstrate the applicability of our method, numerically and experimentally, by engineering shift-variant PSFs via thin plate elements placed in arbitrary planes inside complex imaging systems, performing cascaded optimization of multiple planes, and designing optimal machine-vision systems by deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge