Omar Oubari
A sampling-based approach for efficient clustering in large datasets
Dec 29, 2021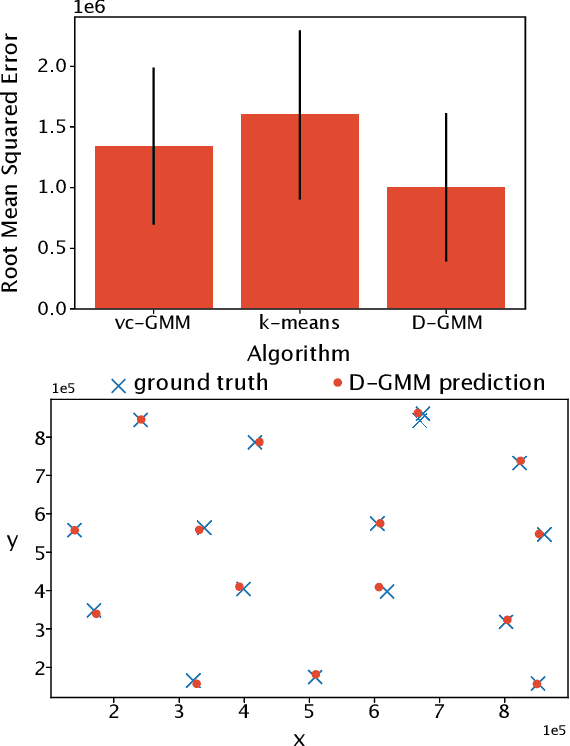
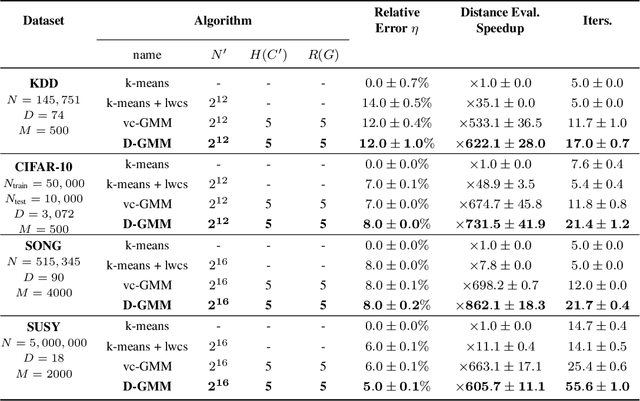
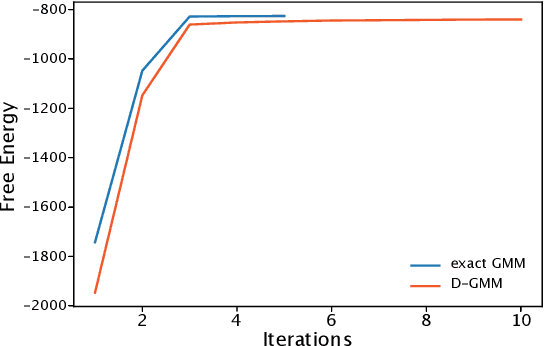
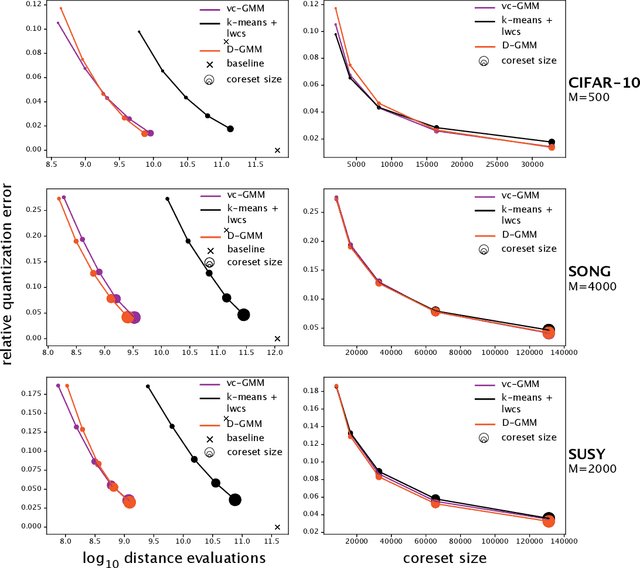
Abstract:We propose a simple and efficient clustering method for high-dimensional data with a large number of clusters. Our algorithm achieves high-performance by evaluating distances of datapoints with a subset of the cluster centres. Our contribution is substantially more efficient than k-means as it does not require an all to all comparison of data points and clusters. We show that the optimal solutions of our approximation are the same as in the exact solution. However, our approach is considerably more efficient at extracting these clusters compared to the state-of-the-art. We compare our approximation with the exact k-means and alternative approximation approaches on a series of standardised clustering tasks. For the evaluation, we consider the algorithmic complexity, including number of operations to convergence, and the stability of the results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge