Efficient Learning Under Density Shift in Incremental Settings Using Cramér-Rao-Based Regularization

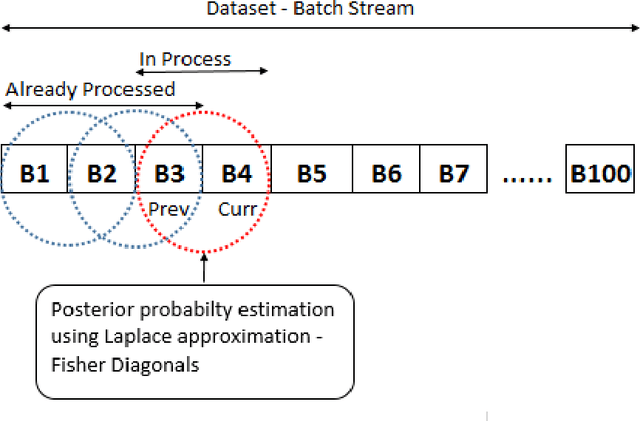
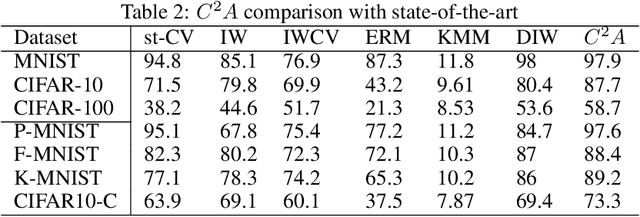
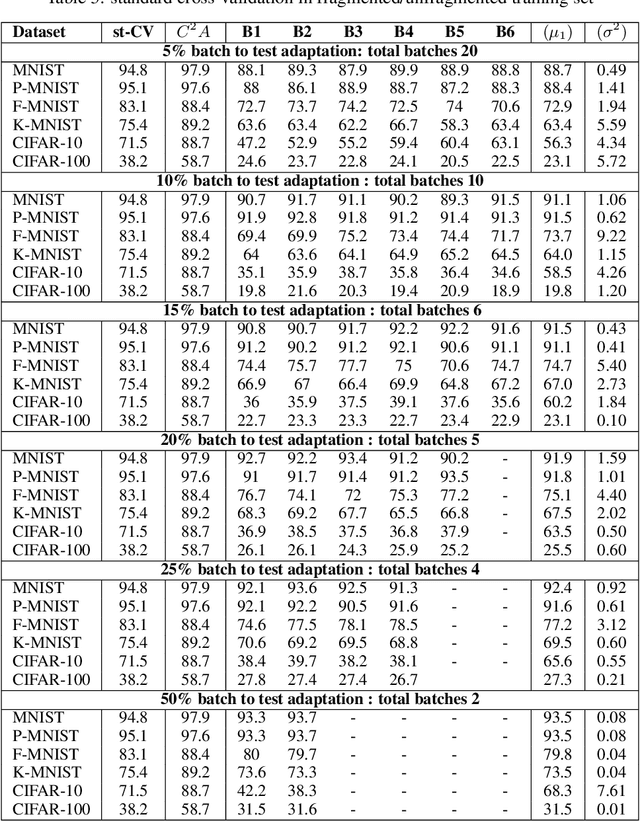
The continuous surge in data volume and velocity is often dealt with using data orchestration and distributed processing approaches, abstracting away the machine learning challenges that exist at the algorithmic level. With growing interest in automating the learning loop, training with data that arrive in a sequence rather than in the classical in-memory training data form will face a machine learning challenge because of evolving feature distributions across batches of training data biasing the cross-validation step (\cite{sugiyama2012machine}). This work takes a distributed density estimation angle to the problem where data are temporally distributed. It processes data in batches and allows a neural network to treat a batch as training data. The method accumulates knowledge about the data density via posterior probability absorption using the Fisher Information Matrix, which contains information about the local optimization gradients for the batch. This is then used as a regularizer for the loss in the following batch, and therefore the density estimate for the entire dataset constructively gets more robust to the non-iid distribution shift. This needs the presence of a pair of batches in memory at a time, so the space cost is not a function of the size of the complete, distributed dataset. We proposed a novel regularization-based approach Covariate Shift Correction $C^{2}A$ that leverages Fisher information and Kullback-Leibler divergence to adapt to both natural and sequential covariate shift caused by dataset fragmentation. $C^{2}A$ achieves $19\%$ accuracy at maximum against state-of-the-art methods.

Mitigating covariate shift in non-colocated data with learned parameter priors

When training data are distributed across{ time or space,} covariate shift across fragments of training data biases cross-validation, compromising model selection and assessment. We present \textit{Fragmentation-Induced covariate-shift Remediation} ($FIcsR$), which minimizes an $f$-divergence between a fragment's covariate distribution and that of the standard cross-validation baseline. We s{how} an equivalence with popular importance-weighting methods. {The method}'s numerical solution poses a computational challenge owing to the overparametrized nature of a neural network, and we derive a Fisher Information approximation. When accumulated over fragments, this provides a global estimate of the amount of shift remediation thus far needed, and we incorporate that as a prior via the minimization objective. In the paper, we run extensive classification experiments on multiple data classes, over $40$ datasets, and with data batched over multiple sequence lengths. We extend the study to the $k$-fold cross-validation setting through a similar set of experiments. An ablation study exposes the method to varying amounts of shift and demonstrates slower degradation with $FIcsR$ in place. The results are promising under all these conditions; with improved accuracy against batch and fold state-of-the-art by more than $5\%$ and $10\%$, respectively.