Convergence analysis and acceleration of the smoothing methods for solving extensive-form games

The extensive-form game has been studied considerably in recent years. It can represent games with multiple decision points and incomplete information, and hence it is helpful in formulating games with uncertain inputs, such as poker. We consider an extended-form game with two players and zero-sum, i.e., the sum of their payoffs is always zero. In such games, the problem of finding the optimal strategy can be formulated as a bilinear saddle-point problem. This formulation grows huge depending on the size of the game, since it has variables representing the strategies at all decision points for each player. To solve such large-scale bilinear saddle-point problems, the excessive gap technique (EGT), a smoothing method, has been studied. This method generates a sequence of approximate solutions whose error is guaranteed to converge at $\mathcal{O}(1/k)$, where $k$ is the number of iterations. However, it has the disadvantage of having poor theoretical bounds on the error related to the game size. This makes it inapplicable to large games. Our goal is to improve the smoothing method for solving extensive-form games so that it can be applied to large-scale games. To this end, we make two contributions in this work. First, we slightly modify the strongly convex function used in the smoothing method in order to improve the theoretical bounds related to the game size. Second, we propose a heuristic called centering trick, which allows the smoothing method to be combined with other methods and consequently accelerates the convergence in practice. As a result, we combine EGT with CFR+, a state-of-the-art method for extensive-form games, to achieve good performance in games where conventional smoothing methods do not perform well. The proposed smoothing method is shown to have the potential to solve large games in practice.

A Stochastic Variance Reduced Gradient using Barzilai-Borwein Techniques as Second Order Information

In this paper, we consider to improve the stochastic variance reduce gradient (SVRG) method via incorporating the curvature information of the objective function. We propose to reduce the variance of stochastic gradients using the computationally efficient Barzilai-Borwein (BB) method by incorporating it into the SVRG. We also incorporate a BB-step size as its variant. We prove its linear convergence theorem that works not only for the proposed method but also for the other existing variants of SVRG with second-order information. We conduct the numerical experiments on the benchmark datasets and show that the proposed method with constant step size performs better than the existing variance reduced methods for some test problems.

A globally convergent fast iterative shrinkage-thresholding algorithm with a new momentum factor for single and multi-objective convex optimization

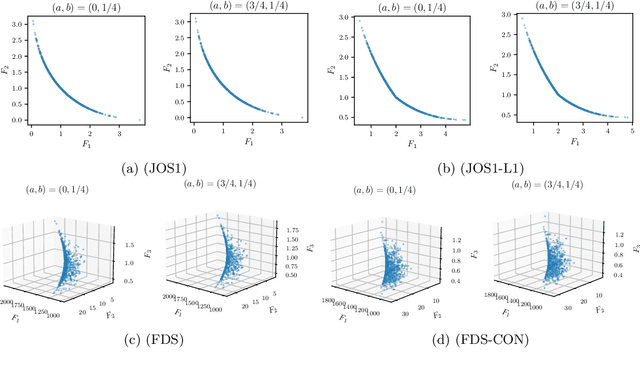
Convex-composite optimization, which minimizes an objective function represented by the sum of a differentiable function and a convex one, is widely used in machine learning and signal/image processing. Fast Iterative Shrinkage Thresholding Algorithm (FISTA) is a typical method for solving this problem and has a global convergence rate of $O(1 / k^2)$. Recently, this has been extended to multi-objective optimization, together with the proof of the $O(1 / k^2)$ global convergence rate. However, its momentum factor is classical, and the convergence of its iterates has not been proven. In this work, introducing some additional hyperparameters $(a, b)$, we propose another accelerated proximal gradient method with a general momentum factor, which is new even for the single-objective cases. We show that our proposed method also has a global convergence rate of $O(1/k^2)$ for any $(a,b)$, and further that the generated sequence of iterates converges to a weak Pareto solution when $a$ is positive, an essential property for the finite-time manifold identification. Moreover, we report numerical results with various $(a,b)$, showing that some of these choices give better results than the classical momentum factors.