Nils Morawietz
Efficient Bayesian Network Structure Learning via Parameterized Local Search on Topological Orderings
Apr 06, 2022
Abstract:In Bayesian Network Structure Learning (BNSL), one is given a variable set and parent scores for each variable and aims to compute a DAG, called Bayesian network, that maximizes the sum of parent scores, possibly under some structural constraints. Even very restricted special cases of BNSL are computationally hard, and, thus, in practice heuristics such as local search are used. A natural approach for a local search algorithm is a hill climbing strategy, where one replaces a given BNSL solution by a better solution within some pre-defined neighborhood as long as this is possible. We study ordering-based local search, where a solution is described via a topological ordering of the variables. We show that given such a topological ordering, one can compute an optimal DAG whose ordering is within inversion distance $r$ in subexponential FPT time; the parameter $r$ allows to balance between solution quality and running time of the local search algorithm. This running time bound can be achieved for BNSL without structural constraints and for all structural constraints that can be expressed via a sum of weights that are associated with each parent set. We also introduce a related distance called `window inversions distance' and show that the corresponding local search problem can also be solved in subexponential FPT time for the parameter $r$. For two further natural modification operations on the variable orderings, we show that algorithms with an FPT time for $r$ are unlikely. We also outline the limits of ordering-based local search by showing that it cannot be used for common structural constraints on the moralized graph of the network.
On the Parameterized Complexity of Polytree Learning
May 20, 2021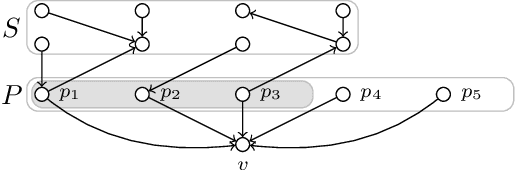
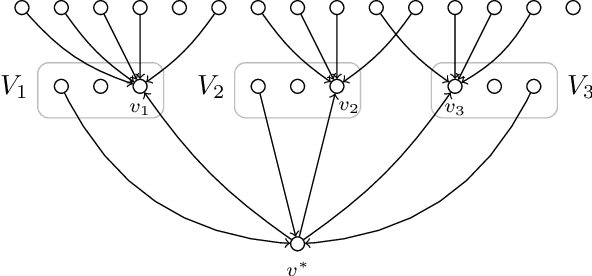
Abstract:A Bayesian network is a directed acyclic graph that represents statistical dependencies between variables of a joint probability distribution. A fundamental task in data science is to learn a Bayesian network from observed data. \textsc{Polytree Learning} is the problem of learning an optimal Bayesian network that fulfills the additional property that its underlying undirected graph is a forest. In this work, we revisit the complexity of \textsc{Polytree Learning}. We show that \textsc{Polytree Learning} can be solved in $3^n \cdot |I|^{\mathcal{O}(1)}$ time where $n$ is the number of variables and $|I|$ is the total instance size. Moreover, we consider the influence of the number of variables $d$ that might receive a nonempty parent set in the final DAG on the complexity of \textsc{Polytree Learning}. We show that \textsc{Polytree Learning} has no $f(d)\cdot |I|^{\mathcal{O}(1)}$-time algorithm, unlike Bayesian network learning which can be solved in $2^d \cdot |I|^{\mathcal{O}(1)}$ time. We show that, in contrast, if $d$ and the maximum parent set size are bounded, then we can obtain efficient algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge