Security Decisions for Cyber-Physical Systems based on Solving Critical Node Problems with Vulnerable Nodes

Cyber-physical production systems consist of highly specialized software and hardware components. Most components and communication protocols are not built according to the Secure by Design principle. Therefore, their resilience to cyberattacks is limited. This limitation can be overcome with common operational pictures generated by security monitoring solutions. These pictures provide information about communication relationships of both attacked and non-attacked devices, and serve as a decision-making basis for security officers in the event of cyberattacks. The objective of these decisions is to isolate a limited number of devices rather than shutting down the entire production system. In this work, we propose and evaluate a concept for finding the devices to isolate. Our approach is based on solving the Critical Node Cut Problem with Vulnerable Vertices (CNP-V) - an NP-hard computational problem originally motivated by isolating vulnerable people in case of a pandemic. To the best of our knowledge, this is the first work on applying CNP-V in context of cybersecurity.

Efficient Bayesian Network Structure Learning via Parameterized Local Search on Topological Orderings

In Bayesian Network Structure Learning (BNSL), one is given a variable set and parent scores for each variable and aims to compute a DAG, called Bayesian network, that maximizes the sum of parent scores, possibly under some structural constraints. Even very restricted special cases of BNSL are computationally hard, and, thus, in practice heuristics such as local search are used. A natural approach for a local search algorithm is a hill climbing strategy, where one replaces a given BNSL solution by a better solution within some pre-defined neighborhood as long as this is possible. We study ordering-based local search, where a solution is described via a topological ordering of the variables. We show that given such a topological ordering, one can compute an optimal DAG whose ordering is within inversion distance $r$ in subexponential FPT time; the parameter $r$ allows to balance between solution quality and running time of the local search algorithm. This running time bound can be achieved for BNSL without structural constraints and for all structural constraints that can be expressed via a sum of weights that are associated with each parent set. We also introduce a related distance called `window inversions distance' and show that the corresponding local search problem can also be solved in subexponential FPT time for the parameter $r$. For two further natural modification operations on the variable orderings, we show that algorithms with an FPT time for $r$ are unlikely. We also outline the limits of ordering-based local search by showing that it cannot be used for common structural constraints on the moralized graph of the network.

On the Parameterized Complexity of Polytree Learning

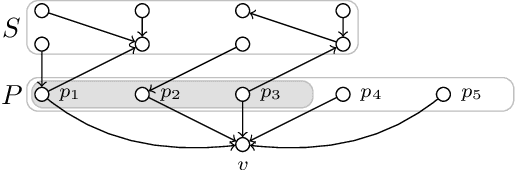
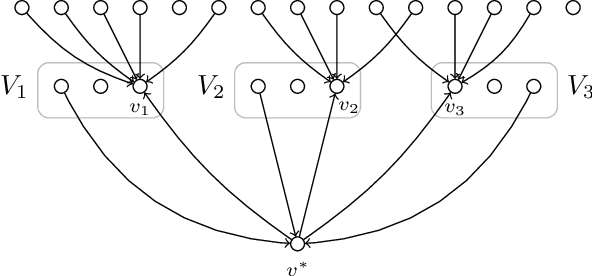
A Bayesian network is a directed acyclic graph that represents statistical dependencies between variables of a joint probability distribution. A fundamental task in data science is to learn a Bayesian network from observed data. \textsc{Polytree Learning} is the problem of learning an optimal Bayesian network that fulfills the additional property that its underlying undirected graph is a forest. In this work, we revisit the complexity of \textsc{Polytree Learning}. We show that \textsc{Polytree Learning} can be solved in $3^n \cdot |I|^{\mathcal{O}(1)}$ time where $n$ is the number of variables and $|I|$ is the total instance size. Moreover, we consider the influence of the number of variables $d$ that might receive a nonempty parent set in the final DAG on the complexity of \textsc{Polytree Learning}. We show that \textsc{Polytree Learning} has no $f(d)\cdot |I|^{\mathcal{O}(1)}$-time algorithm, unlike Bayesian network learning which can be solved in $2^d \cdot |I|^{\mathcal{O}(1)}$ time. We show that, in contrast, if $d$ and the maximum parent set size are bounded, then we can obtain efficient algorithms.

Learning Bayesian Networks Under Sparsity Constraints: A Parameterized Complexity Analysis

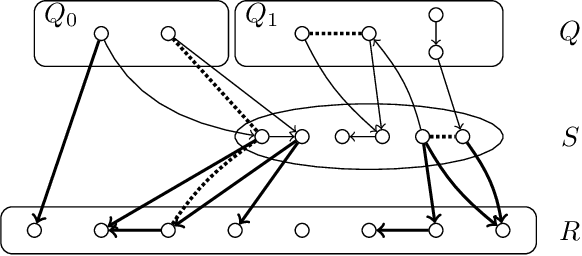
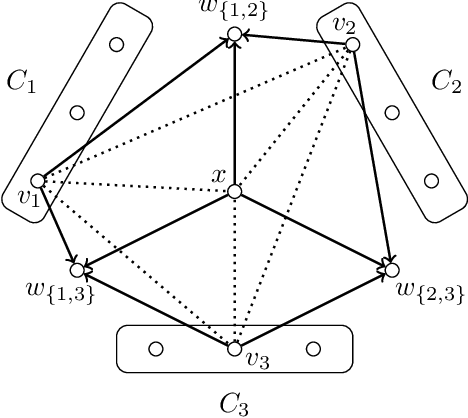
We study the problem of learning the structure of an optimal Bayesian network $D$ when additional constraints are posed on the DAG $D$ or on its moralized graph. More precisely, we consider the constraint that the moralized graph can be transformed to a graph from a sparse graph class $\Pi$ by at most $k$ vertex deletions. We show that for $\Pi$ being the graphs with maximum degree $1$, an optimal network can be computed in polynomial time when $k$ is constant, extending previous work that gave an algorithm with such a running time for $\Pi$ being the class of edgeless graphs [Korhonen & Parviainen, NIPS 2015]. We then show that further extensions or improvements are presumably impossible. For example, we show that when $\Pi$ is the set of graphs with maximum degree $2$ or when $\Pi$ is the set of graphs in which each component has size at most three, then learning an optimal network is NP-hard even if $k=0$. Finally, we show that learning an optimal network with at most $k$ edges in the moralized graph presumably has no $f(k)\cdot |I|^{\mathcal{O}(1)}$-time algorithm and that, in contrast, an optimal network with at most $k$ arcs in the DAG $D$ can be computed in $2^{\mathcal{O}(k)}\cdot |I|^{\mathcal{O}(1)}$ time where $|I|$ is the total input size.