Nikolaj Reiser
Phase Diverse Phase Retrieval for Microscopy: Comparison of Gaussian and Poisson Approaches
Aug 01, 2023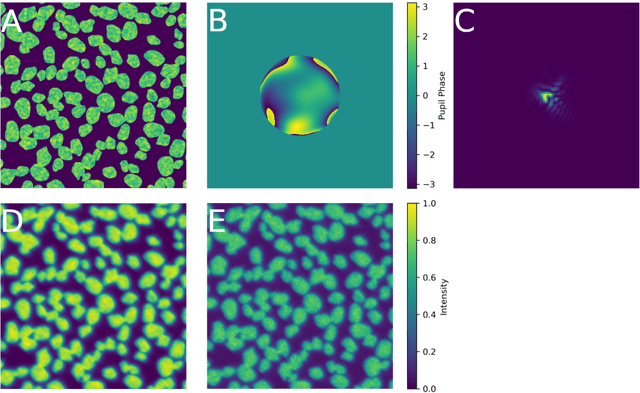

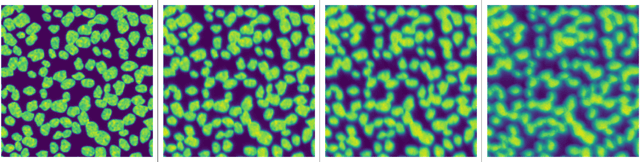

Abstract:Phase diversity is a widefield aberration correction method that uses multiple images to estimate the phase aberration at the pupil plane of an imaging system by solving an optimization problem. This estimated aberration can then be used to deconvolve the aberrated image or to reacquire it with aberration corrections applied to a deformable mirror. The optimization problem for aberration estimation has been formulated for both Gaussian and Poisson noise models but the Poisson model has never been studied in microscopy nor compared with the Gaussian model. Here, the Gaussian- and Poisson-based estimation algorithms are implemented and compared for widefield microscopy in simulation. The Poisson algorithm is found to match or outperform the Gaussian algorithm in a variety of situations, and converges in a similar or decreased amount of time. The Gaussian algorithm does perform better in low-light regimes when image noise is dominated by additive Gaussian noise. The Poisson algorithm is also found to be more robust to the effects of spatially variant aberration and phase noise. Finally, the relative advantages of re-acquisition with aberration correction and deconvolution with aberrated point spread functions are compared.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge