A comparative study of conformal prediction methods for valid uncertainty quantification in machine learning

In the past decades, most work in the area of data analysis and machine learning was focused on optimizing predictive models and getting better results than what was possible with existing models. To what extent the metrics with which such improvements were measured were accurately capturing the intended goal, whether the numerical differences in the resulting values were significant, or whether uncertainty played a role in this study and if it should have been taken into account, was of secondary importance. Whereas probability theory, be it frequentist or Bayesian, used to be the gold standard in science before the advent of the supercomputer, it was quickly replaced in favor of black box models and sheer computing power because of their ability to handle large data sets. This evolution sadly happened at the expense of interpretability and trustworthiness. However, while people are still trying to improve the predictive power of their models, the community is starting to realize that for many applications it is not so much the exact prediction that is of importance, but rather the variability or uncertainty. The work in this dissertation tries to further the quest for a world where everyone is aware of uncertainty, of how important it is and how to embrace it instead of fearing it. A specific, though general, framework that allows anyone to obtain accurate uncertainty estimates is singled out and analysed. Certain aspects and applications of the framework -- dubbed `conformal prediction' -- are studied in detail. Whereas many approaches to uncertainty quantification make strong assumptions about the data, conformal prediction is, at the time of writing, the only framework that deserves the title `distribution-free'. No parametric assumptions have to be made and the nonparametric results also hold without having to resort to the law of large numbers in the asymptotic regime.

Heteroskedastic conformal regression

Conformal prediction, and split conformal prediction as a specific implementation, offer a distribution-free approach to estimating prediction intervals with statistical guarantees. Recent work has shown that split conformal prediction can produce state-of-the-art prediction intervals when focusing on marginal coverage, i.e., on a calibration dataset the method produces on average prediction intervals that contain the ground truth with a predefined coverage level. However, such intervals are often not adaptive, which can be problematic for regression problems with heteroskedastic noise. This paper tries to shed new light on how adaptive prediction intervals can be constructed using methods such as normalized and Mondrian conformal prediction. We present theoretical and experimental results in which these methods are investigated in a systematic way.

Well-calibrated prediction intervals for regression problems

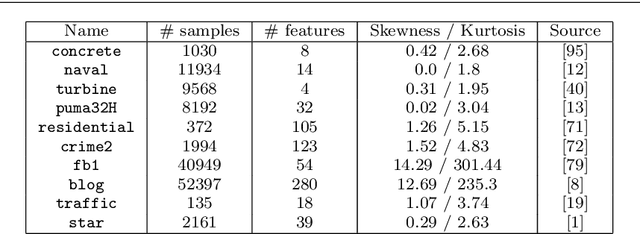
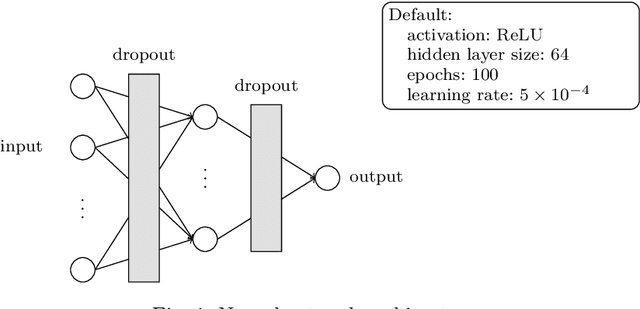
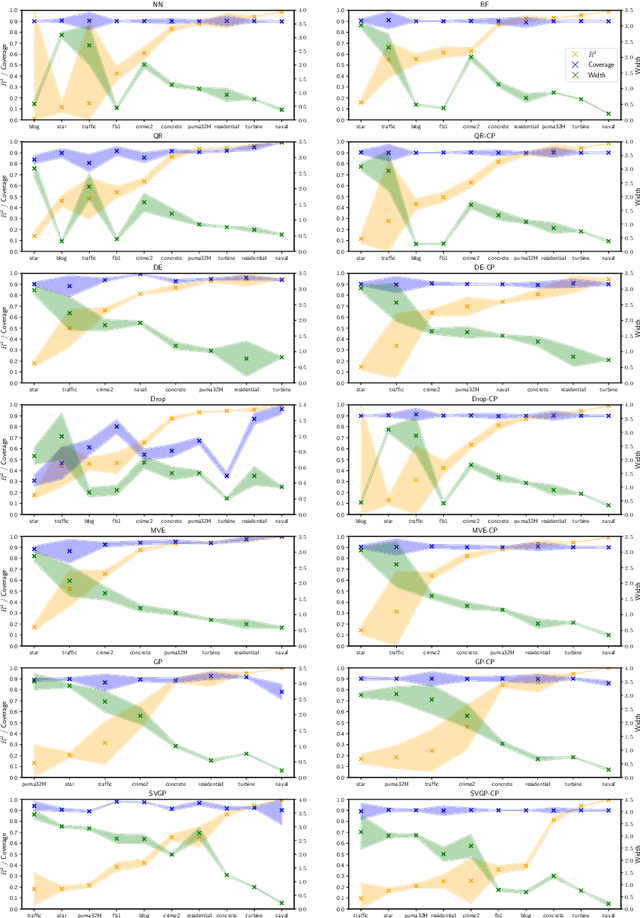
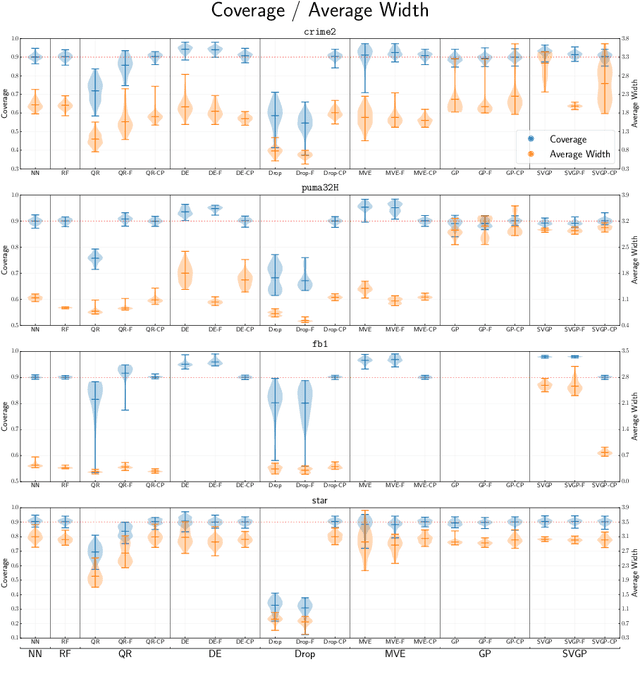
Over the last few decades, various methods have been proposed for estimating prediction intervals in regression settings, including Bayesian methods, ensemble methods, direct interval estimation methods and conformal prediction methods. An important issue is the calibration of these methods: the generated prediction intervals should have a predefined coverage level, without being overly conservative. In this work, we review the above four classes of methods from a conceptual and experimental point of view. Results on benchmark data sets from various domains highlight large fluctuations in performance from one data set to another. These observations can be attributed to the violation of certain assumptions that are inherent to some classes of methods. We illustrate how conformal prediction can be used as a general calibration procedure for methods that deliver poor results without a calibration step.