An evaluation framework for comparing epidemic intelligence systems

In the context of Epidemic Intelligence, many Event-Based Surveillance (EBS) systems have been proposed in the literature to promote the early identification and characterization of potential health threats from online sources of any nature. Each EBS system has its own surveillance definitions and priorities, therefore this makes the task of selecting the most appropriate EBS system for a given situation a challenge for end-users. In this work, we propose a new evaluation framework to address this issue. It first transforms the raw input epidemiological event data into a set of normalized events with multi-granularity, then conducts a descriptive retrospective analysis based on four evaluation objectives: spatial, temporal, thematic and source analysis. We illustrate its relevance by applying it to an Avian Influenza dataset collected by a selection of EBS systems, and show how our framework allows identifying their strengths and drawbacks in terms of epidemic surveillance.

Characterizing and comparing external measures for the assessment of cluster analysis and community detection

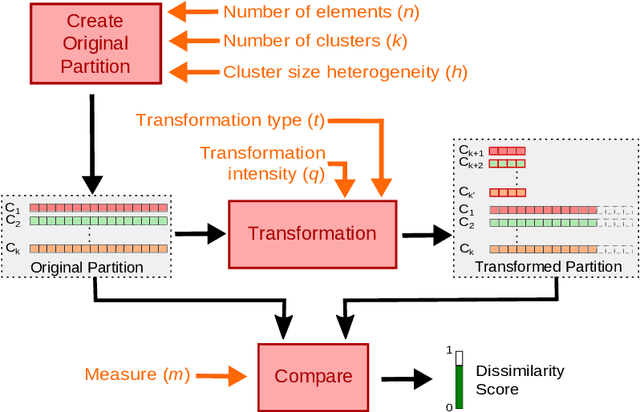
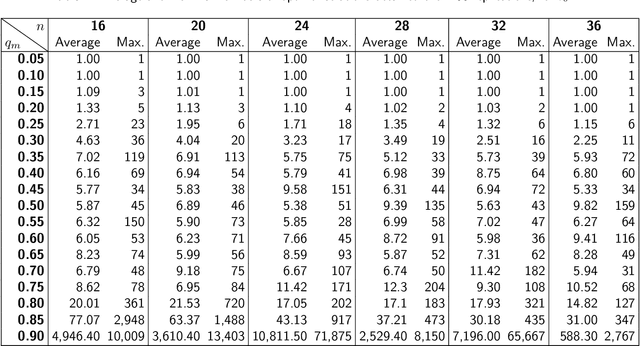
In the context of cluster analysis and graph partitioning, many external evaluation measures have been proposed in the literature to compare two partitions of the same set. This makes the task of selecting the most appropriate measure for a given situation a challenge for the end user. However, this issue is overlooked in the literature. Researchers tend to follow tradition and use the standard measures of their field, although they often became standard only because previous researchers started consistently using them. In this work, we propose a new empirical evaluation framework to solve this issue, and help the end user selecting an appropriate measure for their application. For a collection of candidate measures, it first consists in describing their behavior by computing them for a generated dataset of partitions, obtained by applying a set of predefined parametric partition transformations. Second, our framework performs a regression analysis to characterize the measures in terms of how they are affected by these parameters and transformations. This allows both describing and comparing the measures. Our approach is not tied to any specific measure or application, so it can be applied to any situation. We illustrate its relevance by applying it to a selection of standard measures, and show how it can be put in practice through two concrete use cases.

Multiplicity and Diversity: Analyzing the Optimal Solution Space of the Correlation Clustering Problem on Complete Signed Graphs

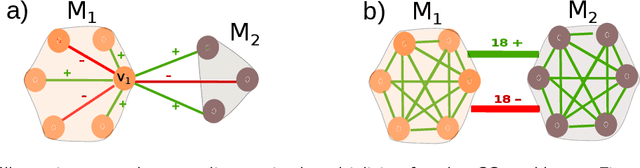
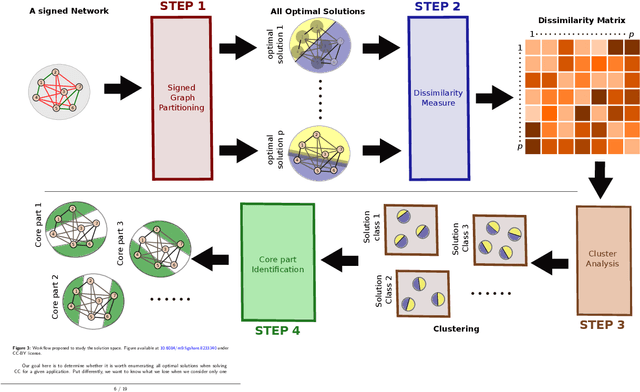
In order to study real-world systems, many applied works model them through signed graphs, i.e. graphs whose edges are labeled as either positive or negative. Such a graph is considered as structurally balanced when it can be partitioned into a number of modules, such that positive (resp. negative) edges are located inside (resp. in-between) the modules. When it is not the case, authors look for the closest partition to such balance, a problem called Correlation Clustering (CC). Due to the complexity of the CC problem, the standard approach is to find a single optimal partition and stick to it, even if other optimal or high scoring solutions possibly exist. In this work, we study the space of optimal solutions of the CC problem, on a collection of synthetic complete graphs. We show empirically that under certain conditions, there can be many optimal partitions of a signed graph. Some of these are very different and thus provide distinct perspectives on the system, as illustrated on a small real-world graph. This is an important result, as it implies that one may have to find several, if not all, optimal solutions of the CC problem, in order to properly study the considered system.