Numerical Computation of Partial Differential Equations by Hidden-Layer Concatenated Extreme Learning Machine

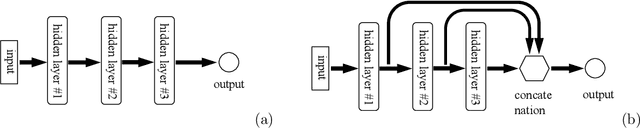
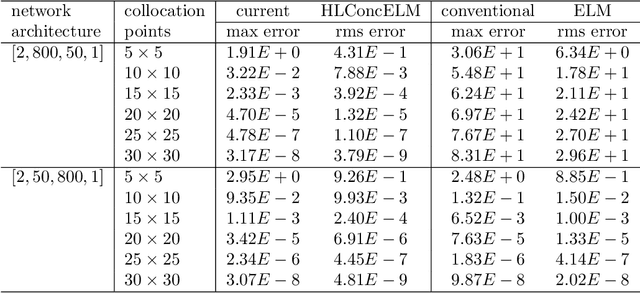
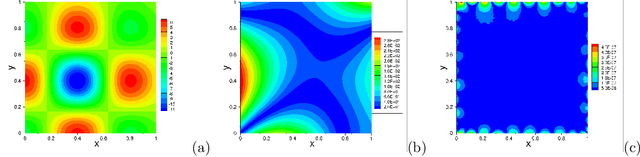
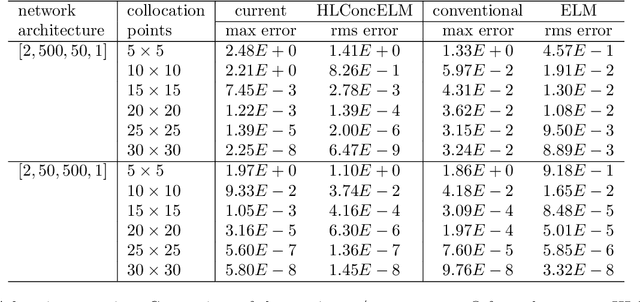
The extreme learning machine (ELM) method can yield highly accurate solutions to linear/nonlinear partial differential equations (PDEs), but requires the last hidden layer of the neural network to be wide to achieve a high accuracy. If the last hidden layer is narrow, the accuracy of the existing ELM method will be poor, irrespective of the rest of the network configuration. In this paper we present a modified ELM method, termed HLConcELM (hidden-layer concatenated ELM), to overcome the above drawback of the conventional ELM method. The HLConcELM method can produce highly accurate solutions to linear/nonlinear PDEs when the last hidden layer of the network is narrow and when it is wide. The new method is based on a type of modified feedforward neural networks (FNN), termed HLConcFNN (hidden-layer concatenated FNN), which incorporates a logical concatenation of the hidden layers in the network and exposes all the hidden nodes to the output-layer nodes. We show that HLConcFNNs have the remarkable property that, given a network architecture, when additional hidden layers are appended to the network or when extra nodes are added to the existing hidden layers, the approximation capacity of the HLConcFNN associated with the new architecture is guaranteed to be not smaller than that of the original network architecture. We present ample benchmark tests with linear/nonlinear PDEs to demonstrate the computational accuracy and performance of the HLConcELM method and the superiority of this method to the conventional ELM from previous works.

A Method for Representing Periodic Functions and Enforcing Exactly Periodic Boundary Conditions with Deep Neural Networks

We present a simple and effective method for representing periodic functions and enforcing exactly the periodic boundary conditions for solving differential equations with deep neural networks (DNN). The method stems from some simple properties about function compositions involving periodic functions. It essentially composes a DNN-represented arbitrary function with a set of independent periodic functions with adjustable (training) parameters. We distinguish two types of periodic conditions: those imposing the periodicity requirement on the function and all its derivatives (to infinite order), and those imposing periodicity on the function and its derivatives up to a finite order $k$ ($k\geqslant 0$). The former will be referred to as $C^{\infty}$ periodic conditions, and the latter $C^{k}$ periodic conditions. We define operations that constitute a $C^{\infty}$ periodic layer and a $C^k$ periodic layer (for any $k\geqslant 0$). A deep neural network with a $C^{\infty}$ (or $C^k$) periodic layer incorporated as the second layer automatically and exactly satisfies the $C^{\infty}$ (or $C^k$) periodic conditions. We present extensive numerical experiments on ordinary and partial differential equations with $C^{\infty}$ and $C^k$ periodic boundary conditions to verify and demonstrate that the proposed method indeed enforces exactly, to the machine accuracy, the periodicity for the DNN solution and its derivatives.