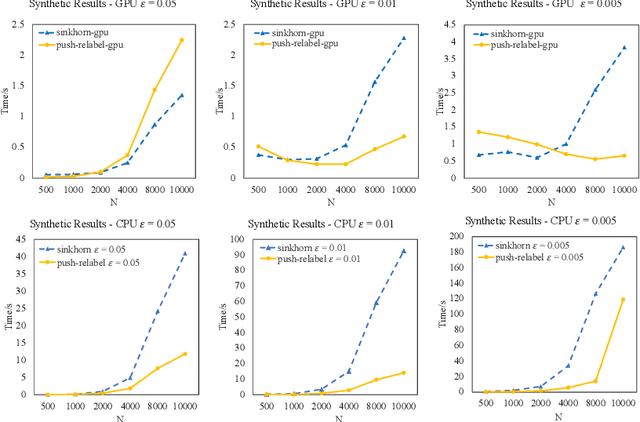
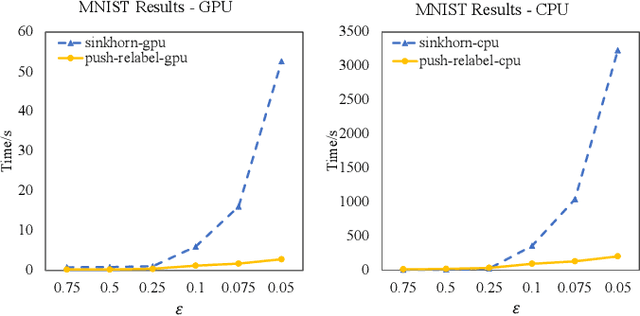
A Push-Relabel Based Additive Approximation for Optimal Transport

Optimal Transport is a popular distance metric for measuring similarity between distributions. Exact algorithms for computing Optimal Transport can be slow, which has motivated the development of approximate numerical solvers (e.g. Sinkhorn method). We introduce a new and very simple combinatorial approach to find an $\varepsilon$-approximation of the OT distance. Our algorithm achieves a near-optimal execution time of $O(n^2/\varepsilon^2)$ for computing OT distance and, for the special case of the assignment problem, the execution time improves to $O(n^2/\varepsilon)$. Our algorithm is based on the push-relabel framework for min-cost flow problems. Unlike the other combinatorial approach (Lahn, Mulchandani and Raghvendra, NeurIPS 2019) which does not have a fast parallel implementation, our algorithm has a parallel execution time of $O(\log n/\varepsilon^2)$. Interestingly, unlike the Sinkhorn algorithm, our method also readily provides a compact transport plan as well as a solution to an approximate version of the dual formulation of the OT problem, both of which have numerous applications in Machine Learning. For the assignment problem, we provide both a CPU implementation as well as an implementation that exploits GPU parallelism. Experiments suggest that our algorithm is faster than the Sinkhorn algorithm, both in terms of CPU and GPU implementations, especially while computing matchings with a high accuracy.

An $\tilde{O}(n^{5/4})$ Time $\varepsilon$-Approximation Algorithm for RMS Matching in a Plane

The 2-Wasserstein distance (or RMS distance) is a useful measure of similarity between probability distributions that has exciting applications in machine learning. For discrete distributions, the problem of computing this distance can be expressed in terms of finding a minimum-cost perfect matching on a complete bipartite graph given by two multisets of points $A,B \subset \mathbb{R}^2$, with $|A|=|B|=n$, where the ground distance between any two points is the squared Euclidean distance between them. Although there is a near-linear time relative $\varepsilon$-approximation algorithm for the case where the ground distance is Euclidean (Sharathkumar and Agarwal, JACM 2020), all existing relative $\varepsilon$-approximation algorithms for the RMS distance take $\Omega(n^{3/2})$ time. This is primarily because, unlike Euclidean distance, squared Euclidean distance is not a metric. In this paper, for the RMS distance, we present a new $\varepsilon$-approximation algorithm that runs in $O(n^{5/4}\mathrm{poly}\{\log n,1/\varepsilon\})$ time. Our algorithm is inspired by a recent approach for finding a minimum-cost perfect matching in bipartite planar graphs (Asathulla et al., TALG 2020). Their algorithm depends heavily on the existence of sub-linear sized vertex separators as well as shortest path data structures that require planarity. Surprisingly, we are able to design a similar algorithm for a complete geometric graph that is far from planar and does not have any vertex separators. Central components of our algorithm include a quadtree-based distance that approximates the squared Euclidean distance and a data structure that supports both Hungarian search and augmentation in sub-linear time.

A Graph Theoretic Additive Approximation of Optimal Transport

Transportation cost is an attractive similarity measure between probability distributions due to its many useful theoretical properties. However, solving optimal transport exactly can be prohibitively expensive. Therefore, there has been significant effort towards the design of scalable approximation algorithms. Previous combinatorial results [Sharathkumar, Agarwal STOC '12, Agarwal, Sharathkumar STOC '14] have focused primarily on the design of strongly polynomial multiplicative approximation algorithms. There has also been an effort to design approximate solutions with additive errors [Cuturi NIPS '13, Altschuler et. al NIPS '17, Dvurechensky et al., ICML '18, Quanrud, SOSA '19] within a time bound that is linear in the size of the cost matrix and polynomial in $C/\delta$; here $C$ is the largest value in the cost matrix and $\delta$ is the additive error. We present an adaptation of the classical graph algorithm of Gabow and Tarjan and provide a novel analysis of this algorithm that bounds its execution time by $O(\frac{n^2 C}{\delta}+ \frac{nC^2}{\delta^2})$. Our algorithm is extremely simple and executes, for an arbitrarily small constant $\varepsilon$, only $\lfloor \frac{2C}{(1-\varepsilon)\delta}\rfloor + 1$ iterations, where each iteration consists only of a Dijkstra search followed by a depth-first search. We also provide empirical results that suggest our algorithm significantly outperforms existing approaches in execution time.