Nathalie Dupuy
Parametric Copula-GP model for analyzing multidimensional neuronal and behavioral relationships
Aug 03, 2020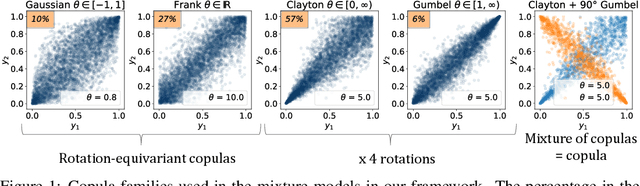

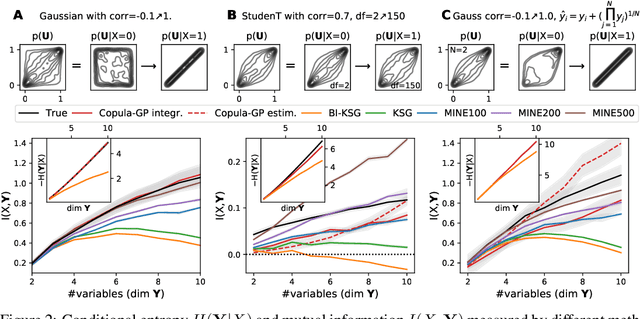
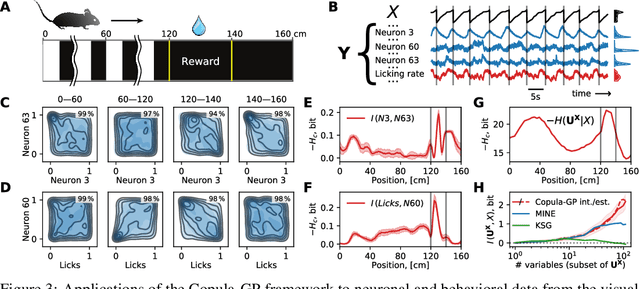
Abstract:One of the main challenges in current systems neuroscience is the analysis of high-dimensional neuronal and behavioral data that are characterized by different statistics and timescales of the recorded variables. We propose a parametric copula model which separates the statistics of the individual variables from their dependence structure, and escapes the curse of dimensionality by using vine copula constructions. We use a Bayesian framework with Gaussian Process (GP) priors over copula parameters, conditioned on a continuous task-related variable. We validate the model on synthetic data and compare its performance in estimating mutual information against the commonly used non-parametric algorithms. Our model provides accurate information estimates when the dependencies in the data match the parametric copulas used in our framework. When the exact density estimation with a parametric model is not possible, our Copula-GP model is still able to provide reasonable information estimates, close to the ground truth and comparable to those obtained with a neural network estimator. Finally, we apply our framework to real neuronal and behavioral recordings obtained in awake mice. We demonstrate the ability of our framework to 1) produce accurate and interpretable bivariate models for the analysis of inter-neuronal noise correlations or behavioral modulations; 2) expand to more than 100 dimensions and measure information content in the whole-population statistics. These results demonstrate that the Copula-GP framework is particularly useful for the analysis of complex multidimensional relationships between neuronal, sensory and behavioral data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge