Automated quantification of one-dimensional nanostructure alignment on surfaces

A method for automated quantification of the alignment of one-dimensional nanostructures from microscopy imaging is presented. Nanostructure alignment metrics are formulated and shown to able to rigorously quantify the orientational order of nanostructures within a two-dimensional domain (surface). A complementary image processing method is also presented which enables robust processing of microscopy images where overlapping nanostructures might be present. Scanning electron microscopy (SEM) images of nanowire-covered surfaces are analyzed using the presented methods and it is shown that past single parameter alignment metrics are insufficient for highly aligned domains. Through the use of multiple parameter alignment metrics, automated quantitative analysis of SEM images is shown to be possible and the alignment characteristics of different samples are able to be rigorously compared using a similarity metric. The results of this work provide researchers in nanoscience and nanotechnology with a rigorous method for the determination of structure/property relationships where alignment of one-dimensional nanostructures is significant.

Theory and Application of Shapelets to the Analysis of Surface Self-assembly Imaging

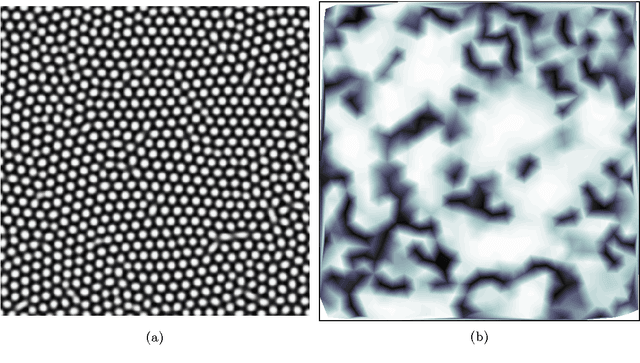
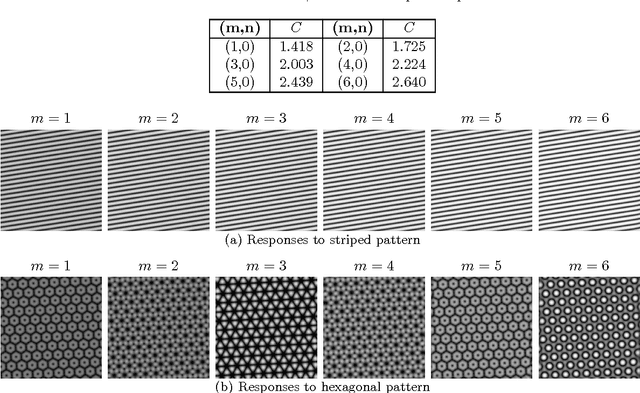
A method for quantitative analysis of local pattern strength and defects in surface self-assembly imaging is presented and applied to images of stripe and hexagonal ordered domains. The presented method uses "shapelet" functions which were originally developed for quantitative analysis of images of galaxies ($\propto 10^{20}\mathrm{m}$). In this work, they are used instead to quantify the presence of translational order in surface self-assembled films ($\propto 10^{-9}\mathrm{m}$) through reformulation into "steerable" filters. The resulting method is both computationally efficient (with respect to the number of filter evaluations), robust to variation in pattern feature shape, and, unlike previous approaches, is applicable to a wide variety of pattern types. An application of the method is presented which uses a nearest-neighbour analysis to distinguish between uniform (defect-free) and non-uniform (strained, defect-containing) regions within imaged self-assembled domains, both with striped and hexagonal patterns.