Post-Training in End-to-End Autonomous Driving

End-to-end models that map multimodal inputs directly to future trajectories/maneuvers have emerged as an increasingly prominent research paradigm in autonomous driving. This class of models includes both Vision-Language-Action models and trajectory-generative planners. Unlike classic machine learning applications, autonomous vehicles operate in safety-critical and interaction-intensive environments where traditional open-loop imitation of expert demonstrations is not sufficient to ensure reliability. In particular, small execution errors can accumulate over time, while recovery behaviors are scarce in training data. In addition, long-horizon objectives such as safety and driving comfort are not captured by pointwise labels either. These limitations have motivated a shift toward post-training techniques, which further refine driving policies beyond pure imitation. This survey presents a unified view of post-training for autonomous driving by defining its scope and organizing the existing literature into four major families based on the form of supervision they use. For each family, we discuss its capabilities, limitations, and open challenges. We aim to facilitate a systematic understanding of this emerging area and stimulate future research on reliable and efficient post-training for autonomous driving.

On the Convergence Rates of Federated Q-Learning across Heterogeneous Environments

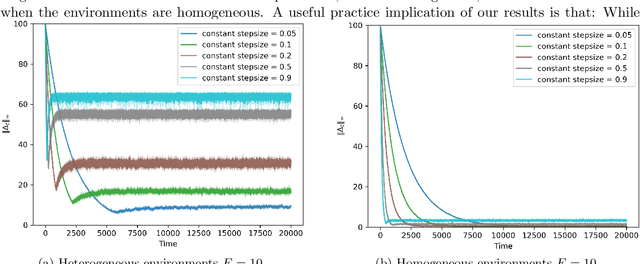
Large-scale multi-agent systems are often deployed across wide geographic areas, where agents interact with heterogeneous environments. There is an emerging interest in understanding the role of heterogeneity in the performance of the federated versions of classic reinforcement learning algorithms. In this paper, we study synchronous federated Q-learning, which aims to learn an optimal Q-function by having $K$ agents average their local Q-estimates per $E$ iterations. We observe an interesting phenomenon on the convergence speeds in terms of $K$ and $E$. Similar to the homogeneous environment settings, there is a linear speed-up concerning $K$ in reducing the errors that arise from sampling randomness. Yet, in sharp contrast to the homogeneous settings, $E>1$ leads to significant performance degradation. Specifically, we provide a fine-grained characterization of the error evolution in the presence of environmental heterogeneity, which decay to zero as the number of iterations $T$ increases. The slow convergence of having $E>1$ turns out to be fundamental rather than an artifact of our analysis. We prove that, for a wide range of stepsizes, the $\ell_{\infty}$ norm of the error cannot decay faster than $\Theta (E/T)$. In addition, our experiments demonstrate that the convergence exhibits an interesting two-phase phenomenon. For any given stepsize, there is a sharp phase-transition of the convergence: the error decays rapidly in the beginning yet later bounces up and stabilizes. Provided that the phase-transition time can be estimated, choosing different stepsizes for the two phases leads to faster overall convergence.