An Empirical Evaluation of the t-SNE Algorithm for Data Visualization in Structural Engineering

A fundamental task in machine learning involves visualizing high-dimensional data sets that arise in high-impact application domains. When considering the context of large imbalanced data, this problem becomes much more challenging. In this paper, the t-Distributed Stochastic Neighbor Embedding (t-SNE) algorithm is used to reduce the dimensions of an earthquake engineering related data set for visualization purposes. Since imbalanced data sets greatly affect the accuracy of classifiers, we employ Synthetic Minority Oversampling Technique (SMOTE) to tackle the imbalanced nature of such data set. We present the result obtained from t-SNE and SMOTE and compare it to the basic approaches with various aspects. Considering four options and six classification algorithms, we show that using t-SNE on the imbalanced data and SMOTE on the training data set, neural network classifiers have promising results without sacrificing accuracy. Hence, we can transform the studied scientific data into a two-dimensional (2D) space, enabling the visualization of the classifier and the resulting decision surface using a 2D plot.

Kernel Ridge Regression Using Importance Sampling with Application to Seismic Response Prediction

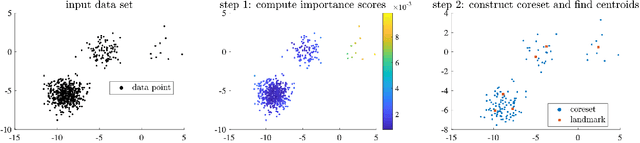
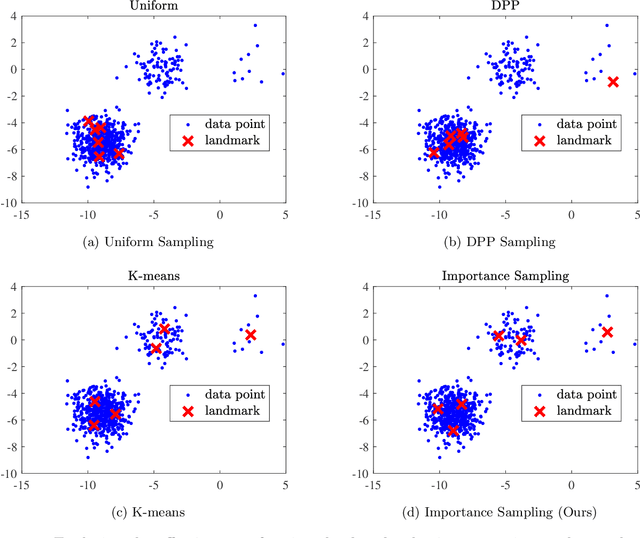
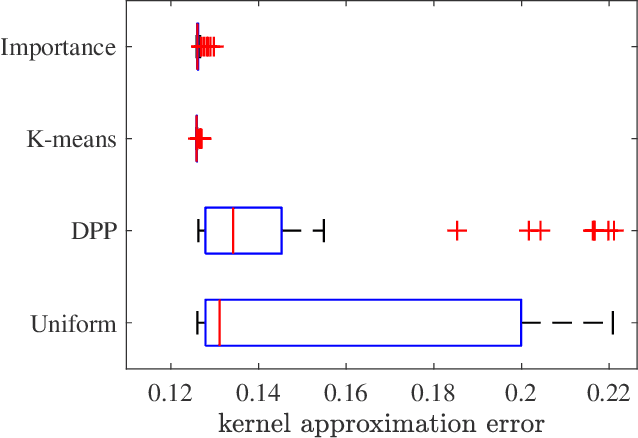
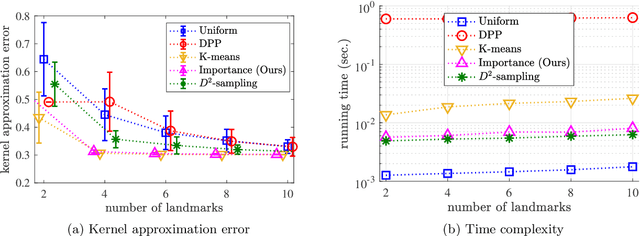
Scalable kernel methods, including kernel ridge regression, often rely on low-rank matrix approximations using the Nystrom method, which involves selecting landmark points from large data sets. The existing approaches to selecting landmarks are typically computationally demanding as they require manipulating and performing computations with large matrices in the input or feature space. In this paper, our contribution is twofold. The first contribution is to propose a novel landmark selection method that promotes diversity using an efficient two-step approach. Our landmark selection technique follows a coarse to fine strategy, where the first step computes importance scores with a single pass over the whole data. The second step performs K-means clustering on the constructed coreset to use the obtained centroids as landmarks. Hence, the introduced method provides tunable trade-offs between accuracy and efficiency. Our second contribution is to investigate the performance of several landmark selection techniques using a novel application of kernel methods for predicting structural responses due to earthquake load and material uncertainties. Our experiments exhibit the merits of our proposed landmark selection scheme against baselines.