Formally Verified Approximate Policy Iteration

We formally verify an algorithm for approximate policy iteration on Factored Markov Decision Processes using the interactive theorem prover Isabelle/HOL. Next, we show how the formalized algorithm can be refined to an executable, verified implementation. The implementation is evaluated on benchmark problems to show its practicability. As part of the refinement, we develop verified software to certify Linear Programming solutions. The algorithm builds on a diverse library of formalized mathematics and pushes existing methodologies for interactive theorem provers to the limits. We discuss the process of the verification project and the modifications to the algorithm needed for formal verification.

Formally Verified Solution Methods for Infinite-Horizon Markov Decision Processes

We formally verify executable algorithms for solving Markov decision processes (MDPs) in the interactive theorem prover Isabelle/HOL. We build on existing formalizations of probability theory to analyze the expected total reward criterion on infinite-horizon problems. Our developments formalize the Bellman equation and give conditions under which optimal policies exist. Based on this analysis, we verify dynamic programming algorithms to solve tabular MDPs. We evaluate the formally verified implementations experimentally on standard problems and show they are practical. Furthermore, we show that, combined with efficient unverified implementations, our system can compete with and even outperform state-of-the-art systems.

Formal Semantics and Formally Verified Validation for Temporal Planning

We present a simple and concise semantics for temporal planning. Our semantics are developed and formalised in the logic of the interactive theorem prover Isabelle/HOL. We derive from those semantics a validation algorithm for temporal planning and show, using a formal proof in Isabelle/HOL, that this validation algorithm implements our semantics. We experimentally evaluate our verified validation algorithm and show that it is practical.

Cost Optimal Planning as Satisfiability

We investigate upper bounds on the length of cost optimal plans that are valid for problems with 0-cost actions. We employ these upper bounds as horizons for a SAT-based encoding of planning with costs. Given an initial upper bound on the cost of the optimal plan, we experimentally show that this SAT-based approach is able to compute plans with better costs, and in many cases it can match the optimal cost. Also, in multiple instances, the approach is successful in proving that a certain cost is the optimal plan cost.

Formally Verified SAT-Based AI Planning

We present an executable formally verified SAT encoding of classical AI planning. We use the theorem prover Isabelle/HOL to perform the verification. We experimentally test the verified encoding and show that it can be used for reasonably sized standard planning benchmarks. We also use it as a reference to test a state-of-the-art SAT-based planner, showing that it sometimes falsely claims that problems have no solutions of certain lengths.

Computing Plan-Length Bounds Using Lengths of Longest Paths

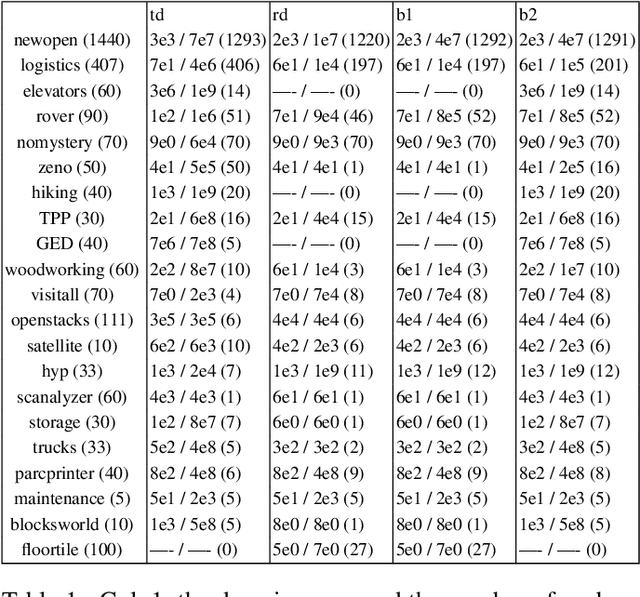
We devise a method to exactly compute the length of the longest simple path in factored state spaces, like state spaces encountered in classical planning. Although the complexity of this problem is NEXP-Hard, we show that our method can be used to compute practically useful upper-bounds on lengths of plans. We show that the computed upper-bounds are significantly (in many cases, orders of magnitude) better than bounds produced by previous bounding techniques and that they can be used to improve the SAT-based planning.