The bi-objective multimodal car-sharing problem

The aim of the bi-objective multimodal car-sharing problem (BiO-MMCP) is to determine the optimal mode of transport assignment for trips and to schedule the routes of available cars and users whilst minimizing cost and maximizing user satisfaction. We investigate the BiO-MMCP from a user-centred point of view. As user satisfaction is a crucial aspect in shared mobility systems, we consider user preferences in a second objective. Users may choose and rank their preferred modes of transport for different times of the day. In this way we account for, e.g., different traffic conditions throughout the planning horizon. We study different variants of the problem. In the base problem, the sequence of tasks a user has to fulfill is fixed in advance and travel times as well as preferences are constant over the planning horizon. In variant 2, time-dependent travel times and preferences are introduced. In variant 3, we examine the challenges when allowing additional routing decisions. Variant 4 integrates variants 2 and 3. For this last variant, we develop a branch-and-cut algorithm which is embedded in two bi-objective frameworks, namely the $\epsilon$-constraint method and a weighting binary search method. Computational experiments show that the branch-and cut algorithm outperforms the MIP formulation and we discuss changing solutions along the Pareto frontier.

Modeling and solving a vehicle-sharing problem

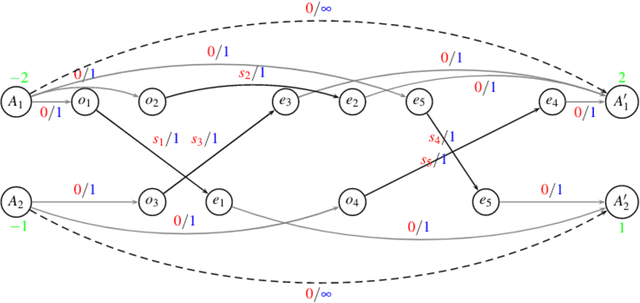
Motivated by the change in mobility patterns, we present a new modeling approach for the vehicle-sharing problem. We aim at assigning vehicles to user-trips so as to maximize savings compared to other modes of transport. We base our formulations on the minimum-cost and the multi-commodity flow problem. These formulations make the problem applicable in daily operations. In the analysis we discuss an optimal composition of a shared fleet, restricted sets of modes of transport, and variations of the objective function.

Modeling and solving the multimodal car- and ride-sharing problem

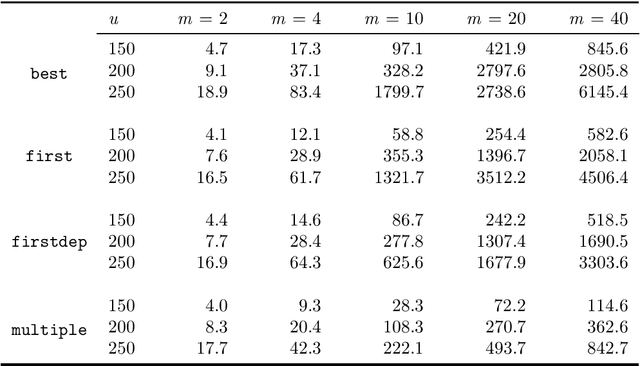
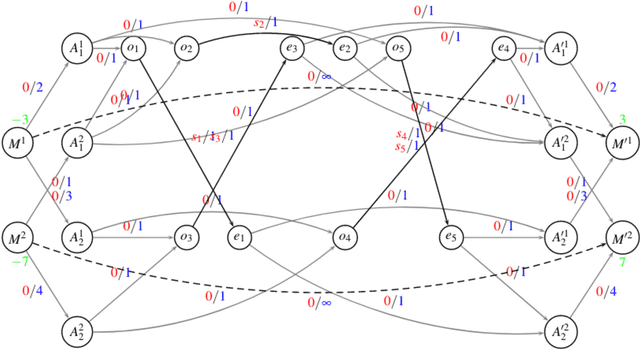
We introduce the multimodal car- and ride-sharing problem (MMCRP), in which a pool of cars is used to cover a set of ride requests, while uncovered requests are assigned to other modes of transport (MOT). A car's route consists of one or more trips. Each trip must have a specific but non-predetermined driver, start in a depot and finish in a (possibly different) depot. Ride-sharing between users is allowed, even when two rides do not have the same origin and/or destination. A user has always the option of using other modes of transport according to an individual list of preferences. The problem can be formulated as a vehicle scheduling problem. In order to solve the problem, an auxiliary graph is constructed in which each trip starting and ending in a depot, and covering possible ride-shares, is modeled as an edge in a time-space graph. We propose a two-layer decomposition algorithm based on column generation, where the master problem ensures that each request can only be covered at most once, and the pricing problem generates new promising routes by solving a kind of shortest path problem in a time-space network. Computational experiments based on realistic instances are reported. The benchmark instances are based on demographic, spatial, and economic data of Vienna, Austria. We solve large instances with the column generation based approach to near optimality in reasonable time, and we further investigate various exact and heuristic pricing schemes.