Milica Orlandic
Quick unsupervised hyperspectral dimensionality reduction for earth observation: a comparison
Feb 26, 2024Abstract:Dimensionality reduction can be applied to hyperspectral images so that the most useful data can be extracted and processed more quickly. This is critical in any situation in which data volume exceeds the capacity of the computational resources, particularly in the case of remote sensing platforms (e.g., drones, satellites), but also in the case of multi-year datasets. Moreover, the computational strategies of unsupervised dimensionality reduction often provide the basis for more complicated supervised techniques. Seven unsupervised dimensionality reduction algorithms are tested on hyperspectral data from the HYPSO-1 earth observation satellite. Each particular algorithm is chosen to be representative of a broader collection. The experiments probe the computational complexity, reconstruction accuracy, signal clarity, sensitivity to artifacts, and effects on target detection and classification of the different algorithms. No algorithm consistently outperformed the others across all tests, but some general trends regarding the characteristics of the algorithms did emerge. With half a million pixels, computational time requirements of the methods varied by 5 orders of magnitude, and the reconstruction error varied by about 3 orders of magnitude. A relationship between mutual information and artifact susceptibility was suggested by the tests. The relative performance of the algorithms differed significantly between the target detection and classification tests. Overall, these experiments both show the power of dimensionality reduction and give guidance regarding how to evaluate a technique prior to incorporating it into a processing pipeline.
A Comparative Study of Compressive Sensing Algorithms for Hyperspectral Imaging Reconstruction
Jan 26, 2024
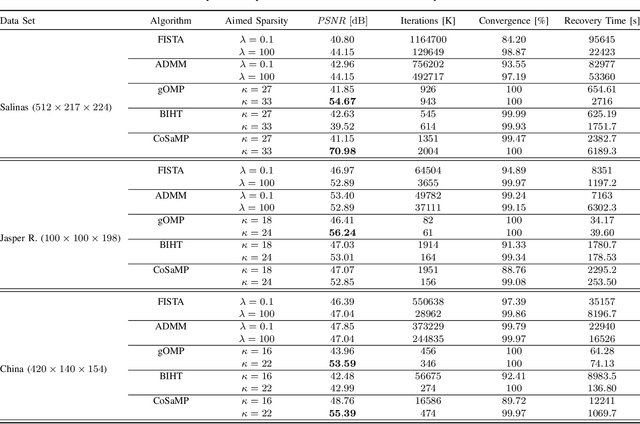
Abstract:Hyperspectral Imaging comprises excessive data consequently leading to significant challenges for data processing, storage and transmission. Compressive Sensing has been used in the field of Hyperspectral Imaging as a technique to compress the large amount of data. This work addresses the recovery of hyperspectral images 2.5x compressed. A comparative study in terms of the accuracy and the performance of the convex FISTA/ADMM in addition to the greedy gOMP/BIHT/CoSaMP recovery algorithms is presented. The results indicate that the algorithms recover successfully the compressed data, yet the gOMP algorithm achieves superior accuracy and faster recovery in comparison to the other algorithms at the expense of high dependence on unknown sparsity level of the data to recover.
Study of the gOMP Algorithm for Recovery of Compressed Sensed Hyperspectral Images
Jan 26, 2024Abstract:Hyperspectral Imaging (HSI) is used in a wide range of applications such as remote sensing, yet the transmission of the HS images by communication data links becomes challenging due to the large number of spectral bands that the HS images contain together with the limited data bandwidth available in real applications. Compressive Sensing reduces the images by randomly subsampling the spectral bands of each spatial pixel and then it performs the image reconstruction of all the bands using recovery algorithms which impose sparsity in a certain transform domain. Since the image pixels are not strictly sparse, this work studies a data sparsification pre-processing stage prior to compression to ensure the sparsity of the pixels. The sparsified images are compressed $2.5\times$ and then recovered using the Generalized Orthogonal Matching Pursuit algorithm (gOMP) characterized by high accuracy, low computational requirements and fast convergence. The experiments are performed in five conventional hyperspectral images where the effect of different sparsification levels in the quality of the uncompressed as well as the recovered images is studied. It is concluded that the gOMP algorithm reconstructs the hyperspectral images with higher accuracy as well as faster convergence when the pixels are highly sparsified and hence at the expense of reducing the quality of the recovered images with respect to the original images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge