Logarithmic Morphological Neural Nets robust to lighting variations

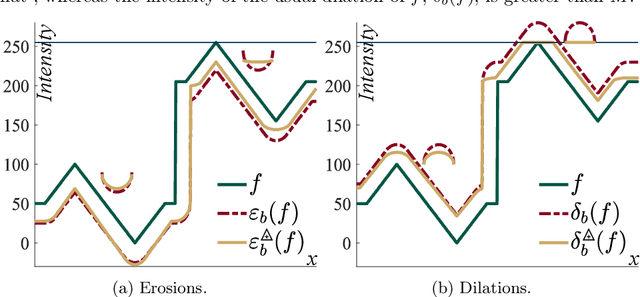
Morphological neural networks allow to learn the weights of a structuring function knowing the desired output image. However, those networks are not intrinsically robust to lighting variations in images with an optical cause, such as a change of light intensity. In this paper, we introduce a morphological neural network which possesses such a robustness to lighting variations. It is based on the recent framework of Logarithmic Mathematical Morphology (LMM), i.e. Mathematical Morphology defined with the Logarithmic Image Processing (LIP) model. This model has a LIP additive law which simulates in images a variation of the light intensity. We especially learn the structuring function of a LMM operator robust to those variations, namely : the map of LIP-additive Asplund distances. Results in images show that our neural network verifies the required property.

Functional Asplund's metrics for pattern matching robust to variable lighting conditions

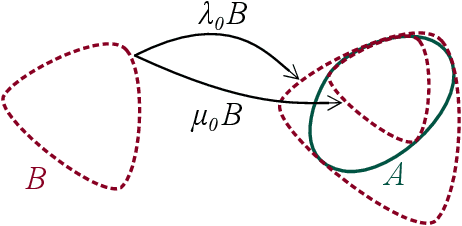
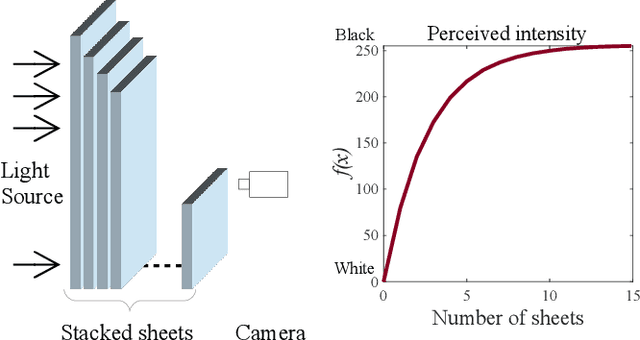
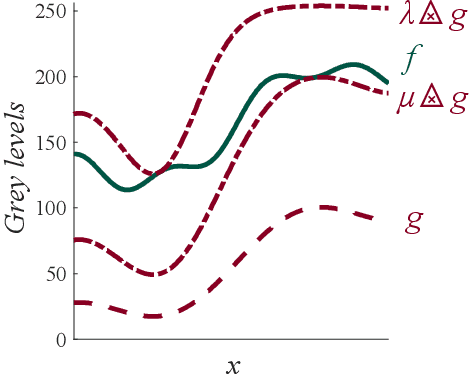
In this paper, we propose a complete framework to process images captured under uncontrolled lighting and especially under low lighting. By taking advantage of the Logarithmic Image Processing (LIP) context, we study two novel functional metrics: i) the LIP-multiplicative Asplund's metric which is robust to object absorption variations and ii) the LIP-additive Asplund's metric which is robust to variations of source intensity and exposure-time. We introduce robust to noise versions of these metrics. We demonstrate that the maps of their corresponding distances between an image and a reference template are linked to Mathematical Morphology. This facilitates their implementation. We assess them in various situations with different lightings and movements. Results show that those maps of distances are robust to lighting variations. Importantly, they are efficient to detect patterns in low-contrast images with a template acquired under a different lighting.

Region homogeneity in the Logarithmic Image Processing framework: application to region growing algorithms

In order to create an image segmentation method robust to lighting changes, two novel homogeneity criteria of an image region were studied. Both were defined using the Logarithmic Image Processing (LIP) framework whose laws model lighting changes. The first criterion estimates the LIP-additive homogeneity and is based on the LIP-additive law. It is theoretically insensitive to lighting changes caused by variations of the camera exposure-time or source intensity. The second, the LIP-multiplicative homogeneity criterion, is based on the LIP-multiplicative law and is insensitive to changes due to variations of the object thickness or opacity. Each criterion is then applied in Revol and Jourlin's (1997) region growing method which is based on the homogeneity of an image region. The region growing method becomes therefore robust to the lighting changes specific to each criterion. Experiments on simulated and on real images presenting lighting variations prove the robustness of the criteria to those variations. Compared to a state-of the art method based on the image component-tree, ours is more robust. These results open the way to numerous applications where the lighting is uncontrolled or partially controlled.

Homogeneity of a region in the logarithmic image processing framework: application to region growing algorithms

The current paper deals with the role played by Logarithmic Image Processing (LIP) operators for evaluating the homogeneity of a region. Two new criteria of heterogeneity are introduced, one based on the LIP addition and the other based on the LIP scalar multiplication. Such tools are able to manage Region Growing algorithms following the Revol's technique: starting from an initial seed, they consist of applying specific dilations to the growing region while its inhomogeneity level does not exceed a certain level. The new approaches we introduce are significantly improving Revol's existing technique by making it robust to contrast variations in images. Such a property strongly reduces the chaining effect arising in region growing processes.

Aspl{ü}nd's metric defined in the Logarithmic Image Processing framework for colour and multivariate images

Aspl{\"u}nd's metric, which is useful for pattern matching, consists in a double-sided probing, i.e. the over-graph and the sub-graph of a function are probed jointly. It has previously been defined for grey-scale images using the Logarithmic Image Processing (LIP) framework. LIP is a non-linear model to perform operations between images while being consistent with the human visual system. Our contribution consists in extending the Aspl{\"u}nd's metric to colour and multivariate images using the LIP framework. Aspl{\"u}nd's metric is insensitive to lighting variations and we propose a colour variant which is robust to noise.

Double-sided probing by map of Asplund's distances using Logarithmic Image Processing in the framework of Mathematical Morphology

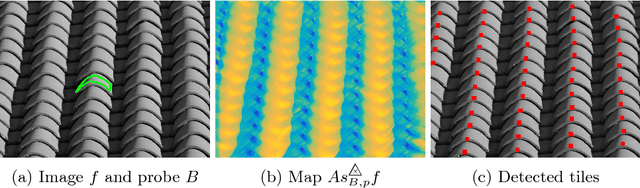
We establish the link between Mathematical Morphology and the map of Asplund's distances between a probe and a grey scale function, using the Logarithmic Image Processing scalar multiplication. We demonstrate that the map is the logarithm of the ratio between a dilation and an erosion of the function by a structuring function: the probe. The dilations and erosions are mappings from the lattice of the images into the lattice of the positive functions. Using a flat structuring element, the expression of the map of Asplund's distances can be simplified with a dilation and an erosion of the image; these mappings stays in the lattice of the images. We illustrate our approach by an example of pattern matching with a non-flat structuring function.

A simple expression for the map of Asplund's distances with the multiplicative Logarithmic Image Processing law

We introduce a simple expression for the map of Asplund's distances with the multiplicative Logarithmic Image Processing (LIP) law. It is a difference between a morphological dilation and a morphological erosion with an additive structuring function which corresponds to a morphological gradient.

Spatio-Colour Asplünd 's Metric and Logarithmic Image Processing for Colour Images (LIPC)

Aspl\"und 's metric, which is useful for pattern matching, consists in a double-sided probing, i.e. the over-graph and the sub-graph of a function are probed jointly. This paper extends the Aspl\"und 's metric we previously defined for colour and multivariate images using a marginal approach (i.e. component by component) to the first spatio-colour Aspl\"und 's metric based on the vectorial colour LIP model (LIPC). LIPC is a non-linear model with operations between colour images which are consistent with the human visual system. The defined colour metric is insensitive to lighting variations and a variant which is robust to noise is used for colour pattern matching.